Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: ĐKXĐ của A là x<>1; x<>-3
ĐKXĐ của B là x<>4
ĐKXĐ của C là x<>0; x<>2
ĐKXĐ của D là x<>3
ĐKXĐ của E là x<>0; x<>2
b: \(A=\dfrac{2x\left(x+3\right)}{\left(x-1\right)\left(x+3\right)}=\dfrac{2x}{x-1}\)
Để A=0 thì 2x=0
=>x=0
\(B=\dfrac{\left(x-4\right)\left(x+4\right)}{\left(x-4\right)^2}=\dfrac{x+4}{x-4}\)
Để B=0 thì x+4=0
=>x=-4
\(C=\dfrac{x\left(x+2\right)}{x\left(x-2\right)}=\dfrac{x+2}{x-2}\)
Để C=0 thì x+2=0
=>x=-2
\(D=\dfrac{\left(x+4\right)\left(x-3\right)}{\left(x-3\right)\left(x^2+3x+9\right)}=\dfrac{x+4}{x^2+3x+9}\)
Để D=0 thi x+4=0
=>x=-4
\(E=\dfrac{2x\left(x^2+2x+1\right)}{2x\left(x-2\right)}=\dfrac{\left(x+1\right)^2}{x-2}\)
Để E=0 thì (x+1)^2=0
=>x=-1

a, \(\left(x-3\right)\left(x^2+x-20\right)\ge0\)
\(\Leftrightarrow\) \(\left(x-3\right)\left(x-4\right)\left(x+5\right)\ge0\)
+) \(x-3=0\Leftrightarrow x=3\); \(x-4=0\Leftrightarrow x=4\); \(x+5=0\Leftrightarrow x=-5\)
+) Lập trục xét dấu f(x) (Bạn tự kẻ trục nha)
\(\Rightarrow\) Bpt có tập nghiệm S = \(\left[-5;3\right]\cup\) [4; \(+\infty\))
b, \(\dfrac{x^2-4x-5}{2x+4}\ge0\)
\(\Leftrightarrow\) \(\dfrac{\left(x-5\right)\left(x+1\right)}{2x+4}\ge0\)
+) \(x-5=0\Leftrightarrow x=5\); \(x+1=0\Leftrightarrow x=-1\); \(2x+4=0\Leftrightarrow x=-2\)
+) Lập trục xét dấu f(x)
\(\Rightarrow\) Bpt có tập nghiệm S = (-2; -1] \(\cup\) [5; \(+\infty\))
c, \(\dfrac{-1}{x^2-6x+8}\le1\)
\(\Leftrightarrow\) \(\dfrac{\left(x-3\right)^2}{\left(x-4\right)\left(x-2\right)}\ge0\)
+) \(x-3=0\Leftrightarrow x=3\); \(x-4=0\Leftrightarrow x=4\); \(x-2=0\Leftrightarrow x=2\)
+) Lập trục xét dấu f(x)
\(\Rightarrow\) Bpt có tập nghiệm S = (\(-\infty\); 2) \(\cup\) (4; \(+\infty\))
Chúc bn học tốt!

Ta có:
f(x) = x4 – x2 + 6x – 9 = x4 – (x2 – 6x +9) = – (x-3)2
= (x2 –x + 3).(x2 + x - 3)
+ Tam thức x2 – x + 3 có Δ = -11 < 0, a = 1 > 0 nên x2 – x + 3 > 0 với ∀ x ∈ R.
+ Tam thức x2 + x – 3 có hai nghiệm 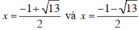
Ta có bảng xét dấu sau:
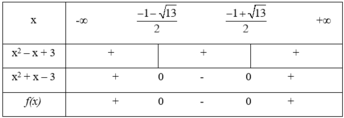
Kết luận:
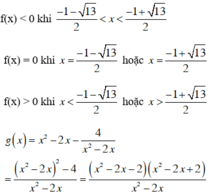
Tam thức x2 - 2x + 2 có Δ = -4 < 0, hệ số a = 1 > 0 nên x2 - 2x + 2 > 0 với ∀ x ∈ R
Tam thức x2 - 2x - 2 có hai nghiệm là x1 = 1 - √3; x2 = 1 + √3.
Tam thức x2 - 2x có hai nghiệm là x1 = 0; x2 = 2
Ta có bảng xét dấu :
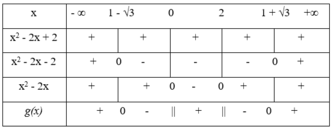
Kết luận : g(x) < 0 khi x ∈ (1 - √3; 0) ∪ (2; 1 + √3)
g(x) = 0 khi x = 1- √3 hoặc x = 1 + √3
g(x) > 0 khi x ∈ (-∞; 1 - √3) ∪ (0; 2) ∪ (1 + √3; +∞)
g(x) không xác định khi x = 0 và x = 2.

Để pt có 2 nghiệm dương (ko yêu cầu pb?) \(\left\{{}\begin{matrix}a\ne0\\\Delta\ge0\\x_1+x_2=-\frac{b}{a}>0\\x_1x_2=\frac{c}{a}>0\end{matrix}\right.\)
a/ \(\left\{{}\begin{matrix}\Delta=\left(2m-1\right)^2+4m-4\ge0\\x_1+x_2=2m+1>0\\x_1x_2=-m+1>0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}4m^2-3\ge0\\m>-\frac{1}{2}\\m< 1\end{matrix}\right.\) \(\Rightarrow\frac{\sqrt{3}}{2}\le m< 1\)
b/ \(\left\{{}\begin{matrix}\Delta=\left(m+2\right)^2-4\left(-2m+1\right)\ge0\\-m-2>0\\-2m+1>0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m^2+12m\ge0\\m< -2\\m< \frac{1}{2}\end{matrix}\right.\) \(\Rightarrow m\le-12\)
e/
\(\left\{{}\begin{matrix}\Delta=\left(m+1\right)^2-4m\ge0\\x_1+x_2=m+1>0\\x_1x_2=m>0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left(m-1\right)^2\ge0\\m>-1\\m>0\end{matrix}\right.\) \(\Rightarrow m>0\)
f/
\(\left\{{}\begin{matrix}m-2\ne0\\\Delta'=\left(2m-3\right)^2-\left(m-2\right)\left(5m-6\right)\ge0\\x_1+x_2=\frac{2\left(3-2m\right)}{m-2}>0\\x_1x_2=\frac{5m-6}{m-2}>0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m\ne2\\-m^2+4m-3\ge0\\\frac{3-2m}{m-2}>0\\\frac{5m-6}{m-2}>0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}m\ne2\\1\le m\le3\\\frac{3}{2}< m< 2\\\left[{}\begin{matrix}m< \frac{6}{5}\\m>2\end{matrix}\right.\end{matrix}\right.\)
\(\Rightarrow\) Không tồn tại m thỏa mãn
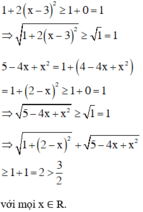
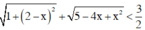 vô nghiệm.
vô nghiệm.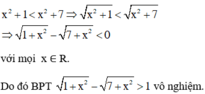
a) Ta có: a = 1 ≠ 0
Δ' = 1 - 3.1= -2 < 0 --> đa thức vô nghiệm.
b) Ta có: a= 4 ≠ 0
Δ' = 22 - 4.7 = -24 < 0 --> vô nghiệm.
c) x.( x +1) +5 = x2 + x +5 . a=1 ≠ 0
Δ= 1 - 5 = -4 < 0 --> vô nghiệm
Câu d) tương tự.....
~ à rề rế ~ ... ko bt làm hay tương tự thật vậy...
câu d khác nhất trong tất cả 4 câu mà...