
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



`a,`
`f(x)=x^2+4x+10`
\(\text{Vì }\)\(x^2\ge0\left(\forall x\right)\)
`->`\(x^2+4x+10\ge10>0\left(\forall\text{ x}\right)\)
`->` Đa thức không có nghiệm (vô nghiệm).
`c,`
`f(x)=5x^4+x^2+` gì nữa bạn nhỉ? Mình đặt vd là 1 đi nha :v.
Vì \(x^4\ge0\text{ }\forall\text{ }x\rightarrow5x^4\ge0\text{ }\forall\text{ }x\)
\(x^2\ge0\text{ }\forall\text{ }x\)
`->`\(5x^4+x^2+1\ge1>0\text{ }\forall\text{ }x\)
`->` Đa thức vô nghiệm.
`b,`
`g(x)=x^2-2x+2017`
Vì \(x^2\ge0\text{ }\forall\text{ }x\)
`->`\(x^2-2x+2017\ge2017\text{ }\forall\text{ }x\)
`->` Đa thức vô nghiệm.
`d,`
`g(x)=4x^2004+x^2018+1`
Vì \(x^{2004}\ge0\text{ }\forall\text{ }x\rightarrow4x^{2004}\ge0\text{ }\forall\text{ }x\)
\(x^{2018}\ge0\text{ }\forall\text{ }x\)
`->`\(4x^{2004}+x^{2018}+1\ge1>0\text{ }\forall\text{ }x\)
`->` Đa thức vô nghiệm.

Có hai cách trình bày với bài này: một là bạn có thể liệt kê hết các phần tử ra hoặc bạn sắp xếp theo cùng thứ tự và tính như sau:


a: =3x^2y^3-2x^3y^2-2xy^4+3x^3y^2+3x^2y^3+5x^4y-5x^3y^2
=6x^2y^3-4x^3y^2-2xy^4+5x^4y
Bậc là 5
b: =x^4-y^4-3x^2y^2-3xy^3+5x^2y^2+x^3y-x^2y^2
=x^4-y^4+x^2y^2-3xy^3+x^3y
Bậc là 4
c: =3x^3y+3x^2y^2-7x^3y+7xy^3-3xy^2+2x^2y^2+5xy+x
=-4x^3y+5x^2y^2+7xy^3-3xy^2+5xy+x
bậc là 4

a, \(x^2\) + 4\(x\) + 10
= ( \(x^2\) + 4\(x\) + 4) + 6
= (\(x\) + 2)2 + 6
vì (\(x\) + 2)2 ≥ 0
⇒ (\(x\) + 2)2 + 6 ≥ 6 > 0 vậy đa thức đã cho vô nghiệm (đpcm)
b, \(x^2\) - 2\(x\) + 5
= (\(x^2\) - 2\(x\) + 1) + 4
= (\(x\) - 1)2 + 4
Vì (\(x\) - 1)2 ≥ 0 ⇒ (\(x\) -1)2 + 4≥ 4 > 0
Vậy đa thức đã cho vô nghiệm (đpcm)

a: \(M\left(x\right)=2x^2+3\)
\(N\left(x\right)=3x^3-2x^2+x\)
b: \(M\left(x\right)+N\left(x\right)=3x^3+x+3\)
\(M\left(x\right)-N\left(x\right)=2x^2+3-3x^3+2x^2-x=-3x^3+2x^2-x+3\)
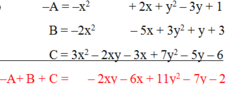
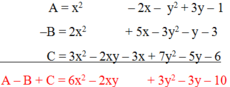
Ta có: x2 +y2 -2x +4y + 6
= x2 - 2x + y2 + 4y + 6
= x2 - x - x + y2 + 2y + 2y + 1 + 4 + 1
=x(x -1) - x + y(y + 2) + 2y + 1 + 4 + 1
=x(x -1) + y(y + 2) - x + 1 + 2y + 4 + 1
=x(x -1) + y(y + 2) - (x - 1) + 2(y + 2) + 1
= (x -1)(x -1) + (y + 2)(y + 2) + 1
=(x -1)2 + (y + 2)2 + 1 >= 1 > 0
Vậy đa thức x2 +y2 -2x +4y +6 ko có nghiệm
x2+y2-2x+4y+6=(x2-2x+1)+(y2+4y+4)+1=(x-1)2+(y+2)2+1>0 với mọi x,y
=>đa thức đã cho vô nghiệm