Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B.
Từ giả thiết, suy ra 5 x + 2 y + 1 3 x y - 1 + x + 1 = 5 x y - 1 + 1 3 x + 2 y + x y - 2 y
⇔ 5 x + 2 y - 1 3 x + 2 y + x + 2 y = 5 x y - 1 - 1 3 x y - 1 + ( x y - 1 ) (1)
Xét hàm số f ( t ) = 5 t - 1 3 t + t trên ℝ .
Đạo hàm f ' ( t ) = 5 t . ln 5 + ln 3 3 t + 1 > 0 , ∀ t ∈ ℝ ⇒ hàm số f (t) luôn đồng biến trên ℝ .
Suy ra 1 ⇔ f ( x + 2 y ) = f ( x y - 1 ) ⇔ x + 2 y = x y - 1 ⇔ x + 1 = y ( x - 2 )
y = x + 1 x - 2
Do y > 0 nên x + 1 x - 2 > 0 ⇔ x > 2 x < - 1 . Mà x > 0 nên x > 2.
Từ đó T = x + y = x + x + 1 x - 2 . Xét hàm số g ( x ) = x + x + 1 x - 2 trên 2 ; + ∞ .
Đạo hàm g ' ( x ) = 1 - 3 x - 2 2 > 0 , g ' ( x ) = 0 ⇔ ( x - 2 ) 2 = 3
⇔ x = 2 + 3 ( t m ) x = 2 - 3 ( L ) . Lập bảng biến thiên của hàm số trên 2 ; + ∞ , ta thấy m i n g ( x ) = g ( 2 + 3 ) = 3 + 2 3 .
Vậy T m i n = 3 + 2 3 khi x = 2 + 3 và y = 1 + 3 .

\(\left(\frac{x^2}{y^2}+2+\frac{y^2}{x^2}\right)-3\left(\frac{x}{y}+\frac{y}{x}\right)+2\ge0\)
\(\left(\frac{x}{y}+\frac{y}{x}\right)^2-3\left(\frac{x}{y}+\frac{y}{x}\right)+2\ge0\)
\(\left(t-1\right)\left(t-2\right)\ge0\) với \(t=\frac{x}{y}+\frac{y}{x}\ge2\)
=>\(\left(t-1\right)\left(t-2\right)\ge0\) luôn đúng với t \(\ge2\) dpcm

Đáp án B
Ta có:
3 x 2 + y 2 − 2 . log 2 x − y = 1 2 1 + log 2 1 − x y ⇔ 3 x 2 + y 2 − 2 . log 2 x − y 2 = log 2 2 − 2 x y
⇔ 3 x 2 + 2 x y + y 2 − 2 + 2 x y . log 2 x − y 2 = log 2 2 − 2 x y ⇔ 3 x − y 2 . log 2 x − y = 3 2 − 2 x y . log 2 2 − 2 x y
Xét hàm số f t = 3 t . log 2 t trên khoảng 0 ; + ∞ , có f ' t = 3 t ln 3. log 2 t + 3 t t . ln 2 > 0 ; ∀ t > 0
Suy ra f t là hàm số đồng biến trên 0 ; + ∞ mà
f x − y 2 = f 2 − 2 x y ⇒ x 2 + y 2 = 2
Khi đó:
M = 2 x 3 + y 3 − 3 x y = 2 x + y x + y 2 − 3 x y − 3 x y ⇔ 2 M = 2 x + y 2 x + y 2 − 3.2 x y − 3.2 x y 2 x + y 2 x + y 2 − 3 x + y 2 + 6 − 3 x + y 2 + 6 = 2 x + y 6 − x + y 2 − 3 x + y 2 + 6 = − 2 a 3 − 3 a 2 + 12 a + 6 ,
Với a = x + y ∈ 0 ; 4
Xét hàm số f a = − 2 a 3 − 3 a 2 + 12 a + 6 trên 0 ; 4 ,
suy ra m ax 0 ; 4 f a = 13.
Vậy giá trị lớn nhất của biểu thức M là 13 2

Đáp án B
Ta có
3 x 2 + y 2 − 2 . log 2 x − y = 1 2 1 + log 2 1 − x y ⇔ 3 x 2 + y 2 − 2 . log 2 x − y 2 = log 2 2 − 2 x y
⇔ 3 x 2 + 2 x y + y 2 − 2 + 2 x y . log 2 x − y 2 = log 2 2 − 2 x y ⇔ 3 x − y 2 . log 2 x − y = 3 2 − 2 x y . log 2 2 − 2 x y
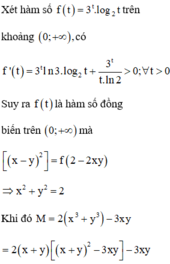
⇔ 2 M = 2 x + y 2 x + y 2 − 3.2. x y − 3.2 x y = 2 x + y 2 x + y 2 − 3 x + y 2 + 6 − 3 x + y 2 + 6
= 2 x + y 6 − x + y 2 − 3 x + y 2 + 6 = − 2 a 3 − 3 a 2 + 12 a + 6 ,
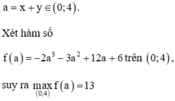
Vậy giá trị lớn nhất của biểu thức M là 13 2

Lời giải:
Ta có $3^m+5^n\equiv 3^m+1\equiv 0\pmod 4$ nên $3^m\equiv (-1)^m\equiv -1\pmod 4$ nên $m$ lẻ
Đặt $m=2k+1$ ( $k\in\mathbb{N}$) thì $3^m=3^{2k+1}\equiv 3\pmod 8$
$\Rightarrow 5^n\equiv 5\pmod 8$. Xét tính chẵn, lẻ ( đặt $n=2t,2t+1$) suy ra $n$ lẻ
Do đó $\Rightarrow 3^n+5^m\equiv (-5)^n+(-3)^m=-(5^n+3^m)\equiv 0\pmod 8$
Ta có đpcm
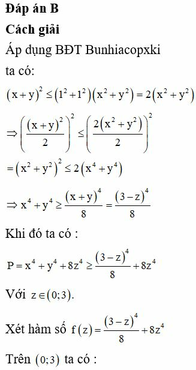

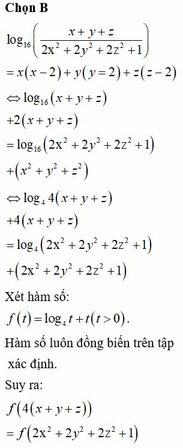



có : (x-y)2 \(\ge0,\forall x,y\)
==>x2-2xy+y2 \(\ge\)0 \(\forall x,y\)
==> 2.(x2+y2)\(\ge\)2xy +x2+y2 \(\forall x,y\)
==> x2+y2 \(\ge\)\(\dfrac{\left(x+y\right)^2}{2}=\dfrac{2^2}{2}=2\) ( do x+y=2) \(\forall x,y\)
lại có (x2-y2)2\(\ge\)0\(\forall x,y\)
==> x4+y4-2x2y2 \(\ge\)0 \(\forall x,y\)
==> 2.(x4+y4) \(\ge\)2x2y2 + x4+y4 \(\forall x,y\)
==> x4+y4 \(\ge\)\(\dfrac{\left(x^2+y^2\right)^2}{2}\ge\dfrac{2^2}{2}=2\)
==> đpcm
dấu ''=,, xảy ra <=> \(\left\{{}\begin{matrix}x+y=2\\x-y=0\\x^2-y^2=0\end{matrix}\right.< =>x=y=1}\)
dấu ''=,, xảy ra <=> x=y=1