Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

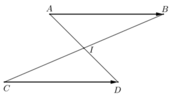
Gọi trung điểm của AD là I, trung điểm BC là J.
Khi đó ta có: 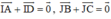
Mà theo quy tắc ba điểm ta có:
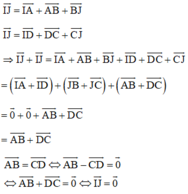
⇔ I ≡ J hay trung điểm AD và BC trùng nhau (đpcm)

Với 4 điểm A, B, C, D ta có: \(\overrightarrow {AB} = \overrightarrow {CD} \) khi và chỉ khi tứ giác ABDC là hình bình hành
Theo tính chất của hình bình hành thì giao điểm của hai đường chéo là trung điểm của mỗi đường và ngược lại.
Nói cách khác: trung điểm của hai đoạn thẳng AD và BC trùng nhau.
Vậy ta có điều phải chứng minh.
Với 4 điểm A, B, C, D ta có: \(\overrightarrow {AB} = \overrightarrow {CD} \) khi và chỉ khi tứ giác ABDC là hình bình hành
Theo tính chất của hình bình hành thì giao điểm của hai đường chéo là trung điểm của mỗi đường và ngược lại.
Nói cách khác: trung điểm của hai đoạn thẳng AD và BC trùng nhau.
Vậy ta có điều phải chứng minh.

Nếu \(\overrightarrow{AB}=\overrightarrow{CD}\) thì AD và BC có trung điểm trùng nhau. Gọi I là trung điểm của AD ta chứng minh I cũng là trung điểm của BC.
Theo quy tắc của ba điểm của tổng, ta có
\(\overrightarrow{AB}=\overrightarrow{AI}+\overrightarrow{IB};\overrightarrow{CD}=\overrightarrow{CI}+\overrightarrow{ID}\)
Vì \(\overrightarrow{AB}=\overrightarrow{CD}\) nên \(\overrightarrow{AI}+\overrightarrow{IB}=\overrightarrow{CI}+\overrightarrow{ID}\)
\(\Rightarrow\overrightarrow{AI}-\overrightarrow{ID}=\overrightarrow{CI}-\overrightarrow{IB}\)
\(\Rightarrow\overrightarrow{AI}+\overrightarrow{DI}=\overrightarrow{CI}+\overrightarrow{BI}\left(1\right)\)
Vì I là trung điểm của AD nên \(\overrightarrow{AI}+\overrightarrow{DI}=\overrightarrow{0}\left(2\right)\)
Từ (1) và (2) suy ra \(\overrightarrow{CI}+\overrightarrow{BI}=\overrightarrow{0}\left(3\right)\)
Từ (3) ta có chung điểm I, ta chứng minh \(\overrightarrow{AB}=\overrightarrow{CD}\)
I là trung điểm AD \(\Rightarrow\overrightarrow{AI}+\overrightarrow{DI}=\overrightarrow{0}\Rightarrow\overrightarrow{AI}-\overrightarrow{ID}=\overrightarrow{0}\)
I là trung điểm BC \(\Rightarrow\overrightarrow{CI}+\overrightarrow{BI}=0\Rightarrow\overrightarrow{CI}-\overrightarrow{IB}=\overrightarrow{0}\)
Suy ra \(\overrightarrow{AI}-\overrightarrow{ID}=\overrightarrow{CI}-\overrightarrow{IB}\)
\(\Rightarrow\overrightarrow{AI}+\overrightarrow{IB}=\overrightarrow{CI}+\overrightarrow{ID}\Rightarrow\overrightarrow{AB}=\overrightarrow{CD}\)

a) \(\overrightarrow{MP}.\overrightarrow{BC}=\dfrac{1}{2}\left(\overrightarrow{MA}+\overrightarrow{MD}\right).\left(\overrightarrow{BM}+\overrightarrow{MC}\right)\)
\(=\dfrac{1}{2}\left(\overrightarrow{MA}.\overrightarrow{BM}+\overrightarrow{MA}.\overrightarrow{MC}+\overrightarrow{MD}.\overrightarrow{BM}+\overrightarrow{MD}.\overrightarrow{MC}\right)\)
\(=\dfrac{1}{2}\left(\overrightarrow{MA}.\overrightarrow{BM}+\overrightarrow{MA}.\overrightarrow{MC}-\overrightarrow{MB}.\overrightarrow{MD}+\overrightarrow{MD}.\overrightarrow{MC}\right)\)
\(=\dfrac{1}{2}\left(\overrightarrow{MA}.\overrightarrow{BM}+\overrightarrow{MD}.\overrightarrow{MC}\right)\)
\(=\dfrac{1}{2}\left(0+0\right)=0\) (vì \(AC\perp BD\) nên \(\overrightarrow{MA}.\overrightarrow{BM}=0;\overrightarrow{MD}.\overrightarrow{MC}=0\)).
Vậy \(\overrightarrow{MP}.\overrightarrow{BC}=0\) nên \(MP\perp BC\).

Xét ΔMDC có N là trung điểm của DC
nên \(2\cdot\overrightarrow{MN}=\overrightarrow{MD}+\overrightarrow{MC}=\overrightarrow{MA}+\overrightarrow{AD}+\overrightarrow{MB}+\overrightarrow{BC}=\overrightarrow{AD}+\overrightarrow{BC}\)

Xét ΔBAD có BM là đường trung tuyến
nên \(\overrightarrow{BM}=\dfrac{1}{2}\left(\overrightarrow{BA}+\overrightarrow{BD}\right)\)
\(=\dfrac{1}{2}\left(\overrightarrow{BA}+\dfrac{2}{3}\overrightarrow{BC}\right)\)
\(=\dfrac{1}{2}\left(\overrightarrow{BA}+\dfrac{2}{3}\overrightarrow{BA}+\dfrac{2}{3}\overrightarrow{AC}\right)\)
\(=\dfrac{1}{2}\left(\dfrac{5}{3}\overrightarrow{BA}+\dfrac{2}{3}\overrightarrow{AC}\right)\)
\(=\dfrac{1}{6}\left(5\overrightarrow{BA}+2\overrightarrow{AC}\right)\)
\(=\dfrac{5}{6}\left(\overrightarrow{BA}+\dfrac{2}{5}\overrightarrow{AC}\right)\)
\(\overrightarrow{BN}=\overrightarrow{BA}+\overrightarrow{AN}\)
\(=\overrightarrow{BA}+\dfrac{2}{5}\overrightarrow{BC}\)
=>\(\overrightarrow{BM}=\dfrac{5}{6}\cdot\overrightarrow{BN}\)
=>B,M,N thẳng hàng

Lấy M là trung điểm của CD
\(AC^2-AD^2=BC^2-BD^2\)
<=> \(\left(\overrightarrow{AC}-\overrightarrow{AD}\right)\left(\overrightarrow{AC}+\overrightarrow{AD}\right)=\left(\overrightarrow{BC}-\overrightarrow{BD}\right)\left(\overrightarrow{BC}+\overrightarrow{BD}\right)\)
<=> \(2.\overrightarrow{DC}.\overrightarrow{AM}=2.\overrightarrow{DC}.\overrightarrow{BM}\)
<=> \(2.\overrightarrow{DC}.\left(\overrightarrow{AM}-\overrightarrow{BM}\right)=0\)
<=> \(2.\overrightarrow{DC}.\overrightarrow{AB}=0\)
<=> DC vuông góc với AB
1/Tìm x biết: (1/2x-1004)^2008 = (1/2x-1004)^2006
2/Cho tam giác ABC cân tại A. D là 1 điểm nằm trong tam giác, biết góc ADB > góc ADC. Chứng minh: DB<DC
giúp e với

Xét ΔBAD có BI là đường trung tuyến
nên \(\overrightarrow{BI}=\dfrac{1}{2}\left(\overrightarrow{BA}+\overrightarrow{BD}\right)\)
=>\(\overrightarrow{BI}=\dfrac{1}{2}\left(\overrightarrow{BA}+\dfrac{2}{3}\overrightarrow{BC}\right)\)
\(=\dfrac{1}{2}\left(\overrightarrow{BA}+\dfrac{2}{3}\overrightarrow{BA}+\dfrac{2}{3}\overrightarrow{AC}\right)\)
\(=\dfrac{1}{2}\left(\dfrac{5}{3}\overrightarrow{BA}+\dfrac{2}{3}\overrightarrow{AC}\right)\)
\(=\dfrac{1}{2}\cdot\dfrac{1}{3}\left(5\overrightarrow{BA}+2\overrightarrow{AC}\right)=\dfrac{1}{6}\left(5\overrightarrow{BA}+2\overrightarrow{AC}\right)=\dfrac{5}{6}\left(\overrightarrow{BA}+\dfrac{2}{5}\overrightarrow{AC}\right)\)
\(\overrightarrow{BM}=\overrightarrow{BA}+\overrightarrow{AM}\)
\(=\overrightarrow{BA}+\dfrac{2}{5}\overrightarrow{AC}\)
=>\(\overrightarrow{BI}=\dfrac{5}{6}\cdot\overrightarrow{BM}\)
=>B,I,M thẳng hàng

Cách 1: Dùng định lý Menelaus đảo:

Từ đề bài, ta có \(\dfrac{BD}{BC}=\dfrac{2}{3}\), \(\dfrac{MC}{MA}=\dfrac{3}{2}\), \(\dfrac{IA}{ID}=1\)
\(\Rightarrow\dfrac{BD}{BC}.\dfrac{MC}{MA}.\dfrac{IA}{ID}=1\)
Theo định lý Menelaus đảo, suy ra B, I, M thẳng hàng.
Cách 2: Dùng vector
Ta có \(\overrightarrow{BI}=\dfrac{1}{2}\left(\overrightarrow{BA}+\overrightarrow{BD}\right)\)
\(=\dfrac{1}{2}\overrightarrow{BA}+\dfrac{1}{2}.\dfrac{2}{3}\overrightarrow{BC}\)
\(=\dfrac{1}{2}\overrightarrow{BA}+\dfrac{1}{3}\overrightarrow{BC}\)
\(=\dfrac{1}{6}\left(3\overrightarrow{BA}+2\overrightarrow{BC}\right)\)
Lại có \(\overrightarrow{BM}=\dfrac{MC}{AC}\overrightarrow{BA}+\dfrac{MA}{AC}\overrightarrow{BC}\)
\(=\dfrac{3}{5}\overrightarrow{BA}+\dfrac{2}{5}\overrightarrow{BC}\)
\(=\dfrac{1}{5}\left(3\overrightarrow{BA}+2\overrightarrow{BC}\right)\)
\(=\dfrac{6}{5}.\dfrac{1}{6}\left(3\overrightarrow{BA}+2\overrightarrow{BC}\right)\)
\(=\dfrac{6}{5}\overrightarrow{BI}\)
Vậy \(\overrightarrow{BM}=\dfrac{6}{5}\overrightarrow{BI}\), suy ra B, I, M thẳng hàng.
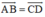
Xét tứ giác ABDC có
AD cắt BC tại trung điểm của mỗi đường
nên ABDC là hình bình hành
Suy ra: vecto AC=vecto BD