Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) \(\overline{ab}+\overline{ba}=10a+b+10b+a=11a+11b=11.\left(a+b\right)\)
Vì 11⋮11 nên \(\overline{ab}+\overline{ba}\)⋮11

b) Ta có: ab+ba =10a+b+10b+a
=11a+11b
Vì 11a chia hết cho 11; 11b chia hết cho 11 nên 11a+11b chia hết cho 11
=> ab+ba chia hết cho 11
c) Ta có: aaabbb= aaax1000+bbb
=111ax1000+111b
=111(ax1000+b)
Vì 111 chia hết cho 37 nên 111(ax1000+b) chia hết cho 37
=> aaabbb chia hết cho 37

a, 10615 + 8 không chia hết cho 2 vì 8 ⋮ 2 nhưng 10615 không chia hết cho 2
10615 + 8 không chia hết cho 9 vì 1 + 6 + 1 + 5 + 8 = 21 không chia hết cho 9
c, B = 102010 - 4
10 \(\equiv\) 1 (mod 3)
102010 \(\equiv\) 12010 (mod 3)
4 \(\equiv\) 1(mod 3)
⇒ 102010 - 4 \(\equiv\) 12010 - 1 (mod 3)
⇒ 102010 - 4 \(\equiv\) 0 (mod 3)
⇒ 102010 - 4 \(⋮\) 3

a)ab+ba
Ta có:ab=10a+b
ba=10b+a
ab+ba=10a+b+10b+a
= 11a + 11b
Ta thấy: 11a⋮11 ; 11b⋮11
=>ab+ba⋮11 (ĐPCM)
b)ab-ba⋮9
Ta có:ab=10a+b
ba=10b+a
ab+ba=10a+b-10b+a
= 9a - 9b
Ta thấy: 9a⋮9 ; 9b⋮9
=>ab+ba⋮9 (ĐPCM)

a, a b + b a = (10a+b)+(10b+a) = 11a+11b = 11.(a+b) ⋮ 11
b, a b - b a = (10a+b) - (10b+a) = 9a - 9b = 9(a - b) ⋮ 9 (a>b)

aaabbb = aaa000 + bbb
= a.111.1000 + b.111
= a.3.37.1000 + b.3.37
= 37.(a.3.1000 + b.3) ⋮ 37
a)
- nếu a và b cùng là số chẵn thì ab(a+b)chia hết cho 2
- nếu a chẵn,b lẻ(hoặc a lẻ,b chẵn)thì ab (a+b) chia hết cho 2
-nếu a và b cùng lẻ thì (a+b) chẵn nên (a+b)chia hết cho 2,vậy ab(a+b) chia hết cho 2
vậy nếu a,b thuộc N thì ab(a+b) chia hết cho 2

a/ ab+ba chia hết cho 11
Vì tổng các số chẵn -tổng các số lẻ:(b+a)-(a+b)=0 chia hết cho 11
=>Tổng ab+ba chia hết cho 11

1. ab+ba
= 10a+b+10b+a
= 11a+11b
= 11(a+b) chia hết cho 11
2. ab-ba
= 10a+b-(10b+a)
= 10a+b-10b-a
= 9a-9b
= 9(a-b) chia hết cho 9
a) ab = 10a + b
ba = 10b + a
=>ab + ba = 11(a+b) chia het cho 11.
b)ab=10a+b
ba=10b+a
ab-ba=9a-9b=9(a-b)=> ab-ba chia hết cho 9
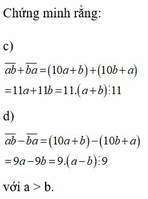
ab+ba=10a+b+10b+a=11a+11b=11.(a+b)
=> ab+ba chia hết cho 11
ab-ba=10a+b-10b+a=9a-9b=9(a-b)
=> ab-ba chia hết cho 9
abcabc=abc.1001=abc.7.11.13
=> abcabc chia hết cho 7;11;13