Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải:
a. $M,N$ đối xứng nhau qua $O$ nghĩa là $O$ là trung điểm $MN$
Tứ giác $AMBN$ có 2 đường chéo $AB, MN$ cắt nhau tại trung điểm $O$ của mỗi đường nên $AMBN$ là hbh $(1)$
Mặt khác, tam giác $ABC$ cân tại $A$ nên trung tuyến $AM$ đồng thời là đường cao
$\Rightarrow AM\perp BC$ nên $\widehat{AMB}=90^0(2)$
Từ $(1); (2)\Rightarrow AMBN$ là hình chữ nhật
b. Vì $AMBN$ là hcn nên $BM\parallel AN$ và $BM=AN$
Mà $B,M,C$ thẳng hàng và $BM=MC$ nên:
$AN\parallel CM, AN=CM$
$\Rightarrow ACMN$ là hình bình hành
c.
$ACMN$ là hbh nên $MN\parallel AC$
Để $ACMN$ là hình vuông thì $MN\perp AB$
$\Leftrightarrow AC\perp AB$
$\Leftrightarrow ABC$ là tam giác vuông tại $A$

a) AM là trung tuyến (gt). => M là trung điểm của BC.
=> BM = MC = \(\dfrac{1}{2}\) BC.
Xét tứ giác AMBN:
I là trung điểm của AB (gt).
I là trung điểm của NM (N là điểm đối xứng với M qua I).
=> Tứ giác AMBN là hình bình hành (dhnb).
=> AN = BM và AN // BM (Tính chất hình bình hành).
Mà BM = MC (cmt).
=> AN = MC.
Xét tứ giác ANMC:
AN = MC (cmt).
AN // MC (AN // BM).
=> Tứ giác ANMC là hình bình hành (dhnb).
b) Xét tam giác ABC vuông tại A:
AM là trung tuyến (gt).
=> AM = \(\dfrac{1}{2}\) BC (Tính chất đường trung tuyến trong tam giác vuông).
Mà BM = MC = \(\dfrac{1}{2}\) BC (cmt).
=> AM = BM = MC = \(\dfrac{1}{2}\) BC.
Xét hình bình hành AMBN: AM = BM (cmt).
=> Tứ giác AMBN là hình thoi (dhnb).
c) Tứ giác ANMC là hình bình hành (cmt).
=> NM = AC (Tính chất hình bình hành).
Mà AC = 6 cm (gt).
=> NM = AC = 6 cm.
\(S_{AMBN}=\dfrac{1}{2}.AB.NM=\dfrac{1}{2}.4.6=12\left(cm^2\right).\)
d) Tứ giác AMBN là hình vuông (gt).
=> \(\widehat{AMB}=90^o\) (Tính chất hình vuông).
=> \(AM\perp BC.\)
Xét tam giác ABC vuông tại A:
AM là trung tuyến (gt).
AM là đường cao \(\left(AM\perp BC\right).\)
=> Tam giác vuông ABC vuông cân tại A.

D. Hình thang có hai góc kề một đáy bằng nhau là hình bình hành.

a) Do AM = DN Þ MADN là hình bình hành
⇒ D ^ = A M N ^ = E M B ^ = M B C ^
Ta có DMPE = DBPE nên EP = FP. Vậy MEBF là hình thoi và 2 điểm E, F đối xứng nhau qua AB.
b) Tứ giác MEBF có MB Ç EF = P; Lại có P trung điểm BM, P là trung điểm EF, MB ^ EF.
Þ MEBF là hình thoi.
c) Để BNCE là hình thang cân thì C N E ^ = B E N ^
Mà
C N E ^ = D ^ = M B C ^ = E B M ^ nên DMEB có 3 góc bằng nhau, suy ra điều kiện để BNCE là hình thang cân thì A B C ^ = 60 0
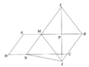

a: M đối xứng N qua AB
nên AM=AN; BM=BN
mà MA=MB
nên MA=MB=AN=BN
=>AMBN là hình thoi
b: Xét tứ giác ACMN có
AN//CM
AN=CM
Do đó: ACMN là hình bình hành
=>AM cắt CN tại trung điểm của mỗi dường
=>N,I,C thẳng hàng
c: BC=2*AM=10cm
=>AB=8cm
\(S_{ABC}=\dfrac{1}{2}\cdot6\cdot8=24\left(cm^2\right)\)
A