Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



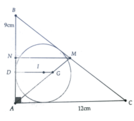
Gọi M là trung điểm của BC
Ta tính được AG = 2 3 AM = 10cm
Gọi N là trung điểm của AB => MN//AC, MN ⊥ AB
D,I,G thẳng hàng
<=> A G A M = A D A N = 2 3 <=> A D 2 A N = 1 3 <=> A D A B = 1 3
Ta có AD = r nội tiếp = A B + A C - B C 2 <=> A B 3 = A B + A C - B C 2
<=> AB+3AC = 3BC = A B 2 + A C 2
<=> 3AC = 4AB (đpcm)
Áp dụng kết quả trên ta có: AD = A B + A C - B C 2 = 3cm
=> ID = DA = 3cm => IG = DG – ID = 1cm

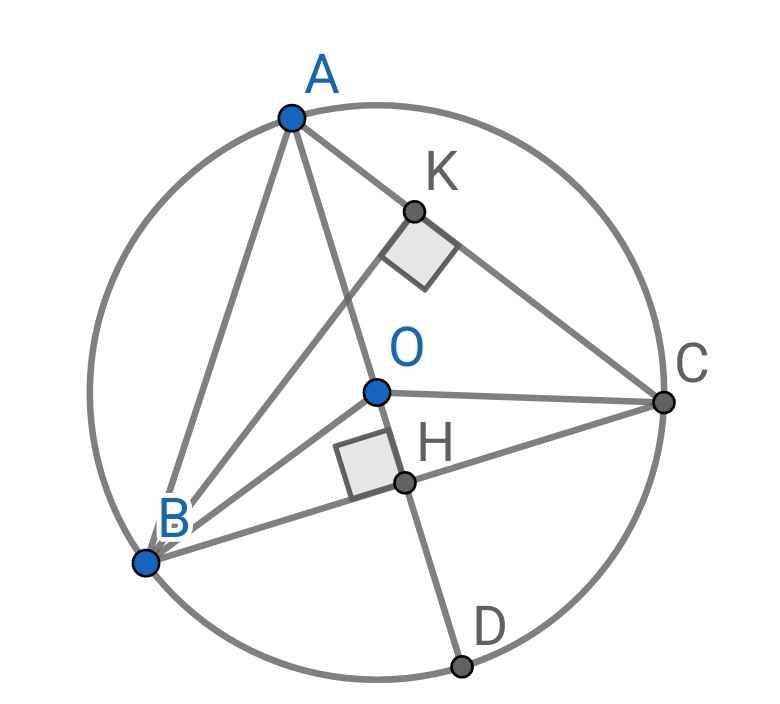 a) Ta có:
a) Ta có:
OB = OC (bán kính)
⇒ O nằm trên đường trung trực của BC (1)
Do ∆ABC cân tại A (gt)
AH là đường cao (gt)
⇒ AH cũng là đường trung trực của ∆ABC
⇒ AH là đường trung trực của BC (2)
Từ (1) và (2) suy ra O ∈ AH
⇒ O ∈ AD
Vậy AD là đường kính của (O)
b) Sửa đề: Tính độ dài các đường cao AH, BK của ∆ABC
Do AH là đường trung trực của BC (cmt)
⇒ H là trung điểm của BC
⇒ CH = BC : 2
= 12 : 2
= 6 (cm)
∆AHC vuông tại H
⇒ AC² = AH² + CH² (Pytago)
⇒ AH² = AC² - CH²
= 10² - 6²
= 64
⇒ AH = 8 (cm)
⇒ sinACH = AH/AC
= 4/5
⇒ ACH ≈ 53⁰
⇒ BCK ≈ 53⁰
∆BCK vuông tại K
⇒ sinBCK = BK/BC
⇒ BK = BC.sinBCK
= 10.sin53⁰
≈ 8 (cm)