K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NV
Nguyễn Việt Lâm
Giáo viên
8 tháng 7 2021
\(P=\dfrac{x-t}{y+t}+\dfrac{y-x}{z+x}+\dfrac{z-y}{t+y}+\dfrac{t-z}{x+z}\)
\(P=\dfrac{x+z-\left(y+t\right)}{y+t}+\dfrac{y+t-\left(z+x\right)}{z+x}=\dfrac{x+z}{y+t}+\dfrac{y+t}{z+x}-2\)
\(P\ge2\sqrt{\dfrac{\left(x+z\right)\left(y+t\right)}{\left(y+t\right)\left(x+z\right)}}-2=0\)
Dấu "=" xảy ra khi \(x+z=y+t\)
LV
1
8 tháng 7 2021
\(xy+yz+zx=3xyz\Leftrightarrow\dfrac{1}{x}+\dfrac{1}{y}+\dfrac{1}{z}=3\)
Có \(\dfrac{1}{x+2y+3z}=\dfrac{1}{\left(x+y\right)+\left(y+z\right)+2z}\le\dfrac{1}{9}\left(\dfrac{1}{x+y}+\dfrac{1}{y+z}+\dfrac{1}{2z}\right)\le\dfrac{1}{9}\left(\dfrac{1}{4x}+\dfrac{1}{4y}+\dfrac{1}{4y}+\dfrac{1}{4z}+\dfrac{1}{2z}\right)=\dfrac{1}{9}\left(\dfrac{1}{4x}+\dfrac{1}{2y}+\dfrac{3}{4z}\right)\)
Tương tự cx có: \(\dfrac{1}{y+2z+3x}\le\dfrac{1}{9}\left(\dfrac{1}{4y}+\dfrac{1}{2z}+\dfrac{3}{4x}\right)\);\(\dfrac{1}{z+2x+3y}\le\dfrac{1}{9}\left(\dfrac{1}{4z}+\dfrac{1}{2x}+\dfrac{3}{4y}\right)\)
Cộng vế với vế \(\Rightarrow\Sigma\dfrac{1}{x+2y+3z}\le\dfrac{1}{9}\left(\dfrac{1}{4}+\dfrac{1}{2}+\dfrac{3}{4}\right)\left(\dfrac{1}{x}+\dfrac{1}{y}+\dfrac{1}{z}\right)=\dfrac{1}{2}\)
Dấu "=" xayra khi x=y=z=1
Vậy \(P_{max}=\dfrac{1}{2}\)
NV
Nguyễn Việt Lâm
Giáo viên
2 tháng 9 2021
\(\sum\dfrac{x^2}{y^2+yz+z^2}\ge\sum\dfrac{x^2}{y^2+\dfrac{y^2+z^2}{2}+z^2}=\dfrac{2}{3}\sum\dfrac{x^2}{y^2+z^2}\ge\dfrac{2}{3}.\dfrac{3}{2}=1\) (BĐT cuối là BĐT Netsbitt)
Câu b là bài IMO 2001 USA, em có thể tìm thấy rất nhiều lời giải
LV
1
29 tháng 11 2021
\(1,\dfrac{1}{1+x}=1-\dfrac{1}{1+y}+1-\dfrac{1}{1+z}=\dfrac{y}{1+y}+\dfrac{z}{1+z}\ge2\sqrt{\dfrac{xy}{\left(1+x\right)\left(1+y\right)}}\)
Cmtt: \(\dfrac{1}{1+y}\ge2\sqrt{\dfrac{xz}{\left(1+x\right)\left(1+z\right)}};\dfrac{1}{1+z}\ge2\sqrt{\dfrac{xy}{\left(1+x\right)\left(1+y\right)}}\)
Nhân VTV
\(\Leftrightarrow\dfrac{1}{\left(1+x\right)\left(1+y\right)\left(1+z\right)}\ge8\sqrt{\dfrac{x^2y^2z^2}{\left(1+x\right)^2\left(1+y\right)^2\left(1+z\right)^2}}\\ \Leftrightarrow\dfrac{1}{\left(1+x\right)\left(1+y\right)\left(1+z\right)}\ge\dfrac{8xyz}{\left(1+x\right)\left(1+y\right)\left(1+z\right)}\\ \Leftrightarrow8xyz\le1\Leftrightarrow xyz\le\dfrac{1}{8}\)
Dấu \("="\Leftrightarrow x=y=z=\dfrac{1}{2}\)
29 tháng 11 2021
\(2,\\ a,2x^2+y^2-2xy=1\\ \Leftrightarrow\left(x-y\right)^2+x^2=1\\ \Leftrightarrow\left(x-y\right)^2=1-x^2\ge0\\ \Leftrightarrow x^2\le1\Leftrightarrow\sqrt{x^2}\le1\Leftrightarrow\left|x\right|\le1\)
NV
Nguyễn Việt Lâm
Giáo viên
1 tháng 12 2018
\(\dfrac{\sqrt{2}}{\sqrt{2x}.\sqrt{y+z}}\ge\dfrac{\sqrt{2}}{\dfrac{2x+y+z}{2}}=\dfrac{2\sqrt{2}}{2x+y+z}\)
\(\Rightarrow A\ge\sum\dfrac{2\sqrt{2}}{2x+y+z}=2\sqrt{2}\sum\dfrac{1}{2x+y+z}\ge2\sqrt{2}.\dfrac{9}{4\left(x+y+z\right)}=\dfrac{18\sqrt{2}}{4.18\sqrt{2}}=\dfrac{1}{4}\)
\(\Rightarrow A_{min}=\dfrac{1}{4}\) khi \(x=y=z=6\sqrt{2}\)
HN
1
SG
24 tháng 4 2023
\(P=\Sigma\dfrac{x}{x+yz}=\Sigma\dfrac{x}{x(x+y+z)+yz}=\Sigma\dfrac{x}{x^2+xy+xz+yz} \\=\Sigma\dfrac{x}{(x+y)(x+z)}=\dfrac{2(xy+yz+zx)}{(x+y)(y+z)(z+x)}\)
Bất đẳng thức phụ: \(\Pi(x+y)\ge\dfrac{8}{9}(\Sigma x)(\Sigma xy)\)
\(\Leftrightarrow \Sigma(x^2y+x^2z-2xyz)\ge0\) ( đúng do AM-GM )
Dấu ''='' xảy ra khi và chỉ khi: \(x=y=z\)
Áp dụng vào bài toán chính:
\(P\le\dfrac{2(xy+yz+zx)}{\dfrac{8}{9}(\Sigma x)(\Sigma xy)}=\dfrac{9}{4}\)
Dấu ''='' xảy ra khi và chỉ khi: \(x=y=z=\dfrac{1}{3}\)
Vậy \(\max P =\dfrac{9}{4} \) khi \(x=y=z=\dfrac{1}{3}\)
AH
Akai Haruma
Giáo viên
11 tháng 7 2021
Lời giải:
Áp dụng BĐT AM-GM:
$\frac{x^3}{y(x+z)}+\frac{y}{2}+\frac{x+z}{4}\geq \frac{3}{2}x$
Tương tự với các phân thức còn lại, cộng theo vế và rút gọn ta được:
$\Rightarrow P=\sum \frac{x^3}{y(x+z)}\geq \frac{x+y+z}{2}$
Tiếp tục áp dụng AM-GM:
$x+y\geq 2\sqrt{xy}$
$y+z\geq 2\sqrt{yz}$
$x+z\geq 2\sqrt{xz}$
$\Rightarrow x+y+z\geq \sqrt{xy}+\sqrt{yz}+\sqrt{xz}=1$
$\Rightarrow P\geq \frac{1}{2}$
Vậy $P_{\min}=\frac{1}{2}$ khi $x=y=z=\frac{1}{3}$
NV
Nguyễn Việt Lâm
Giáo viên
11 tháng 7 2021
\(\dfrac{x^3}{y\left(x+z\right)}+\dfrac{y}{2}+\dfrac{x+z}{4}\ge\dfrac{3x}{2}\)
Tương tự và cộng lại:
\(P+x+y+z\ge\dfrac{3}{2}\left(x+y+z\right)\)
\(\Rightarrow P\ge\dfrac{1}{2}\left(x+y+z\right)\ge\dfrac{1}{2}\left(\sqrt{xy}+\sqrt{yz}+\sqrt{zx}\right)=\dfrac{1}{2}\)
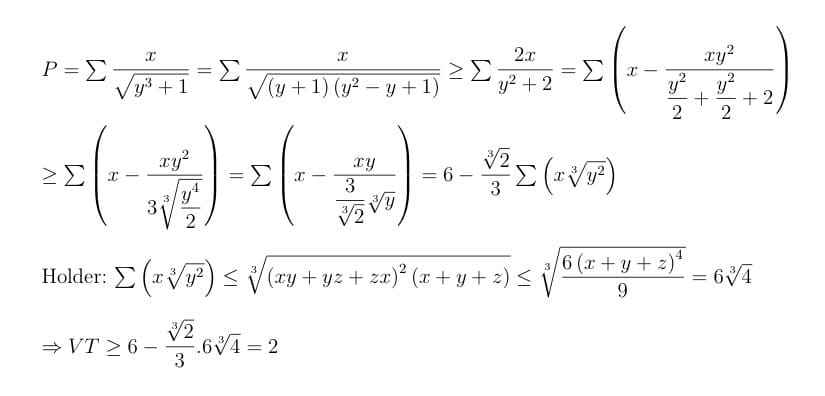
Biểu thức này có min chứ không có max