LP
2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
Y
10 tháng 11 2017
Ta có: x2+y=y2+x
=>x2+y-y2+x=0
=>(x2-y2)-(x-y)=0
=>(x-y)(x+y)-(x-y)=0
=>(x-y)(x+y-1)=0
=>x-y=0 hoặc x+y-1=0
=>x+y=1(TH1 loại do x khác y)
ta có:A=x3+y3+3xy(x2+y2)+6x2y2(x+y)
=>A=(x+y)(x2-xy+y2)+3x3y+3xy3+6x2y2
=>A=x2-xy+y2+3x3y+3xy3+6x2y2
=>A=(x+y)2-3xy+3x2y(x+y)+3xy2(x+y)
=>A=1-3xy+3x2y+3xy2
=>A=1+3xy(-1+a+b)
=>A=1+3xy(-1+1)
=>A=1+3xy.0
=>A=1
Vậy A=1 khi x2+y=y2+x và x khác y.
TQ
2
MT
6 tháng 8 2015
x3+y3=x3+3x2y+3xy2+y2+3xy-3x2y-3xy2
=(x+y)3+3xy.(1-x-y)
=(x+y)3+3xy.[1-(x+y)]
=13+3xy.(1-1)
=1
LT
1
15 tháng 7 2016
\(P=x^3+3xy+y^3=x^3+3xy\left(x+y\right)+y^3=\left(x+y\right)^3=1^3=1\)
NT
a) cho x+y=1. Tính giá trị biểu thức x^3+ y^3+ 3xy
b) cho x-y=1. Tính giá trị biểu thức x^3- y^3- 3xy
2
BT
30 tháng 6 2018
x^3+ y^3+ 3xy
=(x+y)(x^2 -xy + y^2 ) + 3xy
=x^2 -xy + y^2 + 3xy
=x^2 + 2xy + y^2
=(x+y)^2 =1
=> x^3+ y^3+ 3xy=1
TN
13 tháng 6 2016
Từ x+y=1 (GT)
=>(x+y)3=13=1
=>x3+3x2y+3xy2+y3=1 (HĐT)
=>x3+y3+3xy(x+y)=1
=>x3+y3+3xy*1=1
=>x3+y3+3xy=1
13 tháng 6 2016
từ x+y=1=>x=1-y
thay vào biểu thức trên ta được: (1-y)^3+3(1-y)y+y^3=1-3y+3y^2-y^3+3y-3y^2+y^3=1
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
12 tháng 7
13 = (\(x+y\))3 = \(x^3\) + 3\(x^2\)y + 3\(xy^2\) + y3 = \(x^3\)+y3+3\(xy\)(\(x+y\))
1 = \(x^3\)+y3+3\(xy\)
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
12 tháng 7
13 = (\(x-y\))3 = \(x^3\) - 3\(x^2\)y + 3\(xy\) - y3 = \(x^3\) - y3 - 3\(xy\)(\(x-y\))
1 = \(x^3\) - y3 - 3\(xy\)
NT
2
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
12 tháng 7
b; 13 = (\(x-y\))3 = \(x^3\) - 3\(x^2\).y + 3\(xy^2\) - y3 = \(x^3\) - y3 - 3\(xy\)(\(x-y\))
1 = \(x^3\) - y3 - 3\(xy\)
LH
0
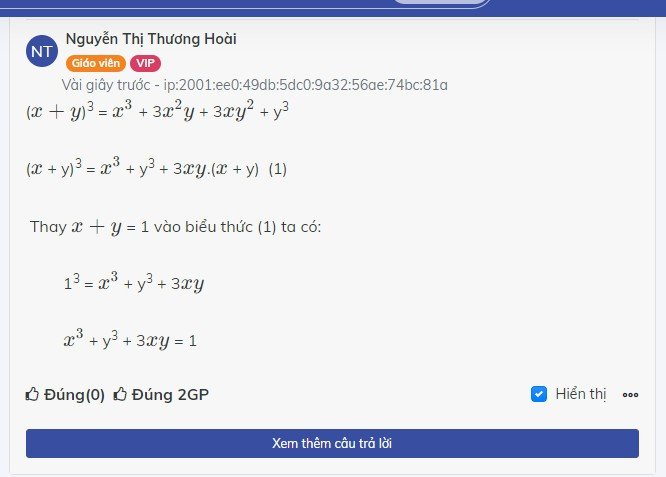
X3 + Y3 = X3 + 3X2Y + 3 XY2+ Y2+ 3XY - 3 X2Y- 3XY2
=(x + y )3 + 3xy. ( 1 - x - y )
=( x + y)3 + 3xy . [ 1 - (x - y) ]
= 13 + 3xy. ( 1-1)
=1
mik cũng ko chắc nữa nhé
Ta có :x3 +y3 +3xy=(x+y)(x2 -xy+y2)+3xy
mà x+y=1
=>x2 -xy+y2+3xy=x2 +2xy+y2 =(x+y)2=12 =1