Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

3x^2+3y^2+4xy-2x+2y+2=0
=>2x^2+4xy+2y^2+x^2-2x+1+y^2+2y+1=0
=>x=1 và y=-1
M=(1-1)^2017+(1-2)^2018+(-1+1)^2015=1

2x2 + 2y2 + 3xy - x + y + 1 = 0
2x2 + 2y2 + 4xy - xy - x + y + 1 = 0
(2x2 + 2y2 + 4xy) + (-xy - x) + (y + 1) = 0
2(x + y)2 - x(y + 1) + (y + 1) = 0
2(x + y)2 + (y + 1)(1 - x) = 0
Do (x + y)2 \(\ge0\)
\(\Rightarrow\) 2(x + y)2 \(\ge0\)
\(\Rightarrow\) 2(x + y)2 + (y + 1)(1 - x) = 0 \(\Leftrightarrow\) (y + 1)(1 - x) = 0
\(\Rightarrow y+1=0;1-x=0\)
*) y + 1 = 0
y = -1
*) 1 - x = 0
x = 1
Với x = 1; y = -1, ta có:
B = [1 + (-1)]2018 + (1 - 2)2018 + (-1 - 1)2018
= 1 + 22018

\(5x2+5y2+8xy-2x+2y+2=0\)
(=) \((4x^2 + 8xy + 4y^2) + (x^2 - 2x +1) + (y^2 + 2y +1) = 0 \)
(=) \(4(x+y)^2 + (x-1)^2 + (y+1)^2 = 0 \)
Ta có \(\begin{cases} 4(x+y)^2 ≥ 0 \\ (x-1)^2 ≥ 0 \\ (y+1)^2 ≥ 0 \end{cases} \)
=> \(4(x+y)^2 + (x-1)^2 + (y+1)^2 ≥ 0 \)
Vậy để \(4(x+y)^2 + (x-1)^2 + (y+1)^2 = 0 \)
(=) \(\begin{cases} 4(x+y)^2 = 0 \\ (x-1)^2 = 0 \\ (y+1)^2 = 0 \end{cases} \)
(=) \(\begin{cases} x = -y \\ x = 1 \\ y = -1 \end{cases} \)
(=) \(\begin{cases} x = 1 \\ y = -1 \end{cases} \)
Vậy \(M=(x+y)^{2015}+(x-2)^{2016}+(y+1)^{2017} M=(1-1)^{2015} + (1-2)^{2016} + (-1+1)^{2017} M=0^{2015} + (-1)^{2016} +0^{2017} M= 1 \)Vậy M = 1

Ta có: \(3x^2+3y^2+4xy+2x-2y+2=0\)
\(\Leftrightarrow x^2+2x+1+y^2-2y+1+2x^2+4xy+2y^2=0\)
\(\Leftrightarrow\left(x+1\right)^2+\left(y-1\right)^2+2\left(x^2+2xy+y^2\right)=0\)
\(\Leftrightarrow\left(x+1\right)^2+\left(y-1\right)^2+2\left(x+y\right)^2=0\)
Ta có: \(\left(x+1\right)^2\ge0\forall x\)
\(\left(y-1\right)^2\ge0\forall y\)
\(2\left(x+y\right)^2\ge0\forall x,y\)
Do đó: \(\left(x+1\right)^2+\left(y-1\right)^2+2\left(x+y\right)^2\ge0\forall x,y\)
Dấu '=' xảy ra khi
\(\left\{{}\begin{matrix}x+1=0\\y-1=0\\x+y=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-1\\y=1\\-1+1=0\left(đúng\right)\end{matrix}\right.\)
Thay x=-1 và y=1 vào biểu thức \(M=\left(x+y\right)^{2016}+\left(x+2\right)^{2017}+\left(y-1\right)^{2018}\), ta được:
\(M=\left(-1+1\right)^{2016}+\left(-1+2\right)^{2017}+\left(1-1\right)^{2018}\)
\(=0^{2016}+1^{2017}+0^{2018}=1\)
Vậy: M=1

a) \(P=3\left(x^2+2xy+y^2\right)-2\left(x+y\right)-100\)
\(P=3\left(x+y\right)^2-2.5-100\)
\(P=3.5^2-110\)
\(P=-35\)
b) \(Q=\left[x^3+y^3+3xy\left(x+y\right)\right]-2\left(x^2+2xy+y^2\right)+3.5+10\)
\(Q=\left(x+y\right)^3-2\left(x+y\right)^2+25\)
\(Q=5^3-2.5^2+25\)
\(Q=100\)
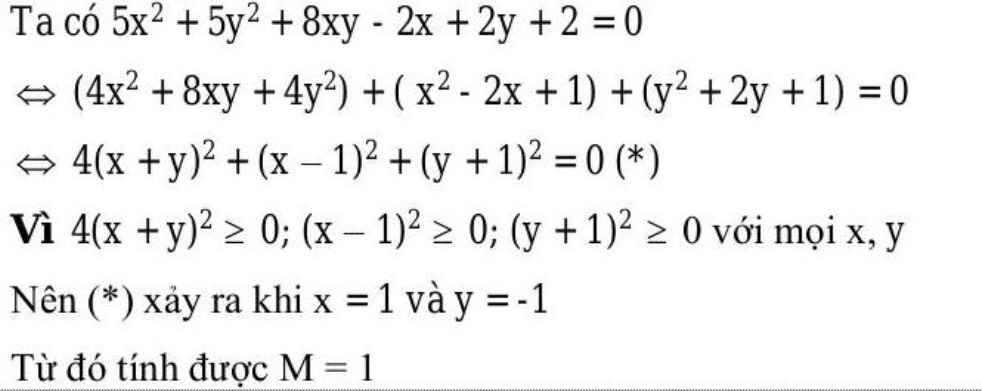
sai/sai đề thì phải