
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\dfrac{M}{3}=\dfrac{x^2+y^2-xy}{x^2+y^2+xy}=\dfrac{3\left(x^2+y^2+xy\right)-2\left(x^2+y^2+2xy\right)}{x^2+y^2+xy}=3-\dfrac{2\left(x+y\right)^2}{x^2+y^2+xy}\le3\)
\(\Rightarrow M\le9\)
\(M_{max}=9\) khi \(\left\{{}\begin{matrix}x+y=0\\x^2+y^2+xy=3\end{matrix}\right.\) \(\Rightarrow\left(x;y\right)=\left(-\sqrt{3};\sqrt{3}\right);\left(\sqrt{3};-\sqrt{3}\right)\)
\(\dfrac{M}{3}=\dfrac{x^2+y^2-xy}{x^2+y^2+xy}=\dfrac{\dfrac{1}{3}\left(x^2+y^2+xy\right)+\dfrac{2}{3}\left(x^2+y^2-2xy\right)}{x^2+y^2+xy}=\dfrac{1}{3}+\dfrac{2\left(x-y\right)^2}{3\left(x^2+y^2+xy\right)}\ge\dfrac{1}{3}\)
\(\Rightarrow M\ge1\)
\(M_{min}=1\) khi \(\left\{{}\begin{matrix}x-y=0\\x^2+y^2+xy=3\end{matrix}\right.\) \(\Rightarrow x=y=\pm1\)

\(x^2+y^2-2x-4y-4=0\\ \Leftrightarrow\left(x-1\right)^2+\left(y-2\right)^2-9=0\\ \Leftrightarrow\left(x-1\right)^2+\left(y-2\right)^2=9=0^2+3^2=0^2+\left(-3\right)^2\\ \Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x-1=0\\y-2=3\end{matrix}\right.\\\left\{{}\begin{matrix}x-1=3\\y-2=0\end{matrix}\right.\\\left\{{}\begin{matrix}x-1=0\\y-2=-3\end{matrix}\right.\\\left\{{}\begin{matrix}x-1=-3\\y-2=0\end{matrix}\right.\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x=1\\y=5\end{matrix}\right.\\\left\{{}\begin{matrix}x=4\\y=2\end{matrix}\right.\\\left\{{}\begin{matrix}x=1\\y=-1\end{matrix}\right.\\\left\{{}\begin{matrix}x=-2\\y=2\end{matrix}\right.\end{matrix}\right.\\ \Leftrightarrow-2\le x\le4\left(y\in R\right)\)
Ta có \(S=3x+4y\)
Mà \(x\ge-2;y\ge-1\Leftrightarrow S\ge3\cdot\left(-2\right)+4\cdot\left(-1\right)=-6-4=-10\)
Vậy GTNN của S là \(-10\Leftrightarrow\left\{{}\begin{matrix}x=-2\\y=-1\end{matrix}\right.\)
Lời giải:
ĐKĐB $\Leftrightarrow (x^2-2x+1)+(y^2-4y+4)-9=0$
$\Leftrightarrow (x-1)^2+(y-2)^2-9=0$
$\Rightarrow (x-1)^2=9-(y-2)^2\leq 9$
$\Rightarrow -3\leq x-1\leq 3$
$\Leftrightarrow -2\leq x\leq 4$
-------------
Đặt $x-1=a; y-2=b$ thì bài toán trở thành:
Cho $a,b$ thực thỏa mãn $a^2+b^2=9$
Tìm min $S=3a+4b+11$
Áp dụng BĐT Bunhiacopxky:
$(3a+4b)^2\leq (a^2+b^2)(3^2+4^2)=9.25$
$\Rightarrow -15\leq 3a+4b\leq 15$
$\Rightarrow 3a+4b\geq -15$
$\Rightarrow S=3a+4b+11\geq -4$
Vậy $S_{\min}=-4$ khi $x=\frac{-4}{5}; y=\frac{-1}{5}$


a) Đây không phải là phương trình đường tròn do có \(xy\).
b) Vì \({a^2} + {b^2} - c = {1^2} + {2^2} - 5 = 0\)nên phương trình đã cho không là phương trình tròn.
c) Vì \({a^2} + {b^2} - c = {\left( { - 3} \right)^2} + {4^2} - 1 = 24 > 0\)nên phương trình đã cho là phương trình tròn có tâm \(I\left( { - 3;4} \right)\) và bán kính \(R = \sqrt {{a^2} + {b^2} - c} = 2\sqrt 6 \).


Tọa độ giao điểm là nghiệm của hệ phương trình
x 2 + y 2 − 6 x − 4 y + 9 = 0 x 2 + y 2 − 2 x − 8 y + 13 = 0 ⇔ x 2 + y 2 − 6 x − 4 y + 9 = 0 − 4 x + 4 y − 4 = 0 ⇔ x 2 + y 2 − 6 x − 4 y + 9 = 0 ( 1 ) x − y + 1 = 0 ( 2 )
Từ (2) suy ra: y = x+ 1 thay vào (1) ta được:
x 2 + ( x + 1 ) 2 - 6 x – 4 ( x + 1 ) + 9 = 0 x 2 + x 2 + 2 x + 1 - 6 x - 4 x – 4 + 9 = 0
2 x 2 – 8 x + 6 = 0
Vậy 2 đường tròn đã cho cắt nhau tại 2 điểm là (1; 2) và (3;4).
ĐÁP ÁN B

Tọa độ giao điểm của đường thẳng và đường tròn là nghiệm của hệ phương trình sau
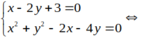
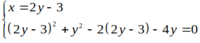
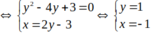 hoặc
hoặc 
Vậy tọa độ giao điểm là (3;3) và (-1; 1) .
Chọn A.

Đáp án: C
Ta có:
(C): x 2 + y 2 + 2x + 4y = 0 ⇔ (x + 1 ) 2 + (y + 2 ) 2 = 5
⇒ I(-1;-2), R = 5
Vì d’ song song với d nên d': 2x + y + c = 0, (c ≠ -3)
Đường thẳng d’ tiếp xúc với (C) nên
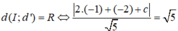
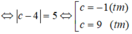
Vậy phương trình đường thẳng d’ là: 2x + y - 1 = 0 hoặc 2x + y + 9 = 0

\(x^2+y^2\le2x+4y\Leftrightarrow\left(x-1\right)^2+\left(y-2\right)^2\le5\)
Trong hệ tọa độ \(Oxy\)vẽ đường tròn \(\left(x-1\right)^2+\left(y-2\right)^2=5\)(C) và đường thẳng \(2x+y-F=0\)(d)
\(F=2x+y\)đạt GTNN hay GTLN khi (d) là tiếp tuyến của (C).
\(I\left(1,2\right)\)là tâm của (C), \(R=\sqrt{5}\)là bán kính của (C).
\(d\left(I,d\right)=\frac{\left|2.1+2-F\right|}{\sqrt{2^2+1^2}}=\frac{\left|F-4\right|}{\sqrt{5}}=\sqrt{5}\Leftrightarrow\orbr{\begin{cases}F=-1\\F=9\end{cases}}\).
Vậy \(minF=-1,maxF=9\).