
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Chọn B
Giả sử hệ bpt có nghiệm duy nhất thì
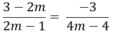
Suy ra: 8m2 - 26m + 15= 0 hay m= ¾ hoặc m= 5/2
Thử lại
+ Với m= ¾ thỏa mãn hệ bpt
+ Với m= 5/2 không thỏa mãn hệ bpt
Vậy m= ¾ là giá trị cần tìm

Phương trình hoành độ giao điểm:
\(x^2-2\left(m+1\right)x+m^2+2=0\)
\(\Delta'=\left(m+1\right)^2-\left(m^2+2\right)=2m-1\ge0\Rightarrow m\ge\dfrac{1}{2}\)
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=2\left(m+1\right)\\x_1x_2=m^2+2\end{matrix}\right.\)
\(A=\sqrt{2\left(x_1+x_2\right)^2-4x_1x_2+16}-3x_1x_2\)
\(A=\sqrt{8\left(m+1\right)^2-4\left(m^2+2\right)+16}-3\left(m^2+2\right)\)
\(A=\sqrt{4m^2+16m+16}-3\left(m^2+2\right)\)
\(A=2m+4-3\left(m^2+2\right)\)
\(A=-3m^2+2m-2=-3m^2+2m-\dfrac{1}{4}-\dfrac{7}{4}\)
\(A=\left(\dfrac{1}{2}-m\right)\left(3m+\dfrac{1}{2}\right)-\dfrac{7}{4}\le-\dfrac{7}{4}\)
\(A_{max}=-\dfrac{7}{4}\) khi \(m=\dfrac{1}{2}\)

Bài 1:
\(c,\text{PT có 2 }n_0\text{ phân biệt }\Leftrightarrow\Delta'=2^2-2m>0\Leftrightarrow2m< 4\Leftrightarrow m< 2\)

Ta có :
\(\left\{{}\begin{matrix}\left(m+1\right)x+my=2m-1\\mx-y=m^2-2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}y=mx-m^2+2\\\left(m+1\right)x+m\left(mx-m^2+2\right)=2m-1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}y=mx-m^2+2\\mx+x+m^2x-m^3+2m=2m-1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}y=mx-m^2+2\\x\left(m+m^2+1\right)=m^3-1\end{matrix}\right.\)
Để hệ pt có nghiệm duy nhất :
\(\Leftrightarrow m^2+m+1>0\)
\(\Leftrightarrow\left(m+\frac{1}{2}\right)^2+\frac{3}{4}>0\) (luôn đúng)
Khi đó hệ pt có nghiệm duy nhất là :
\(\left\{{}\begin{matrix}x=m-1\\y=2-m\end{matrix}\right.\)
Vậy...
Ta có :
\(P=\left(m-1\right)\left(2-m\right)\)
\(=2m-m^2-2+m\)
\(=3m-m^2-2\)
\(=\frac{1}{4}-\left(m-\frac{3}{2}\right)^2\le\frac{1}{4}\)
Dấu "=" xảy ra \(\Leftrightarrow x=\frac{3}{2}\)
Vậy...

- Từ PT ( II ) ta có : \(xy\left(x+y\right)=2xy=4m^2-2m\)
\(\Rightarrow xy=2m^2-m\)
- Hệ PT trên có nghiệm là nghiệm của PT :
\(x^2-2x+2m^2-m=0\) ( I )
Có : \(\Delta^,=b^{,2}-ac=1-\left(2m^2-m\right)=-2m^2+m-1\)
- Để PT ( i ) có nghiệm \(\Leftrightarrow\Delta^,>0\)
\(\Leftrightarrow-2m^2+m-1>0\)
Vậy không tồn tại m để hệ phương trình có nghiệm .
Phương trình (i) có nghiệm $\Leftrightarrow \Delta\geq 0$ chứ không phải $>0$ bạn nhé.
Bạn kiểm tra lại đề, nếu x và y theo m đúng thế này thì \(xy\) chỉ có GTNN chứ không có GTLN