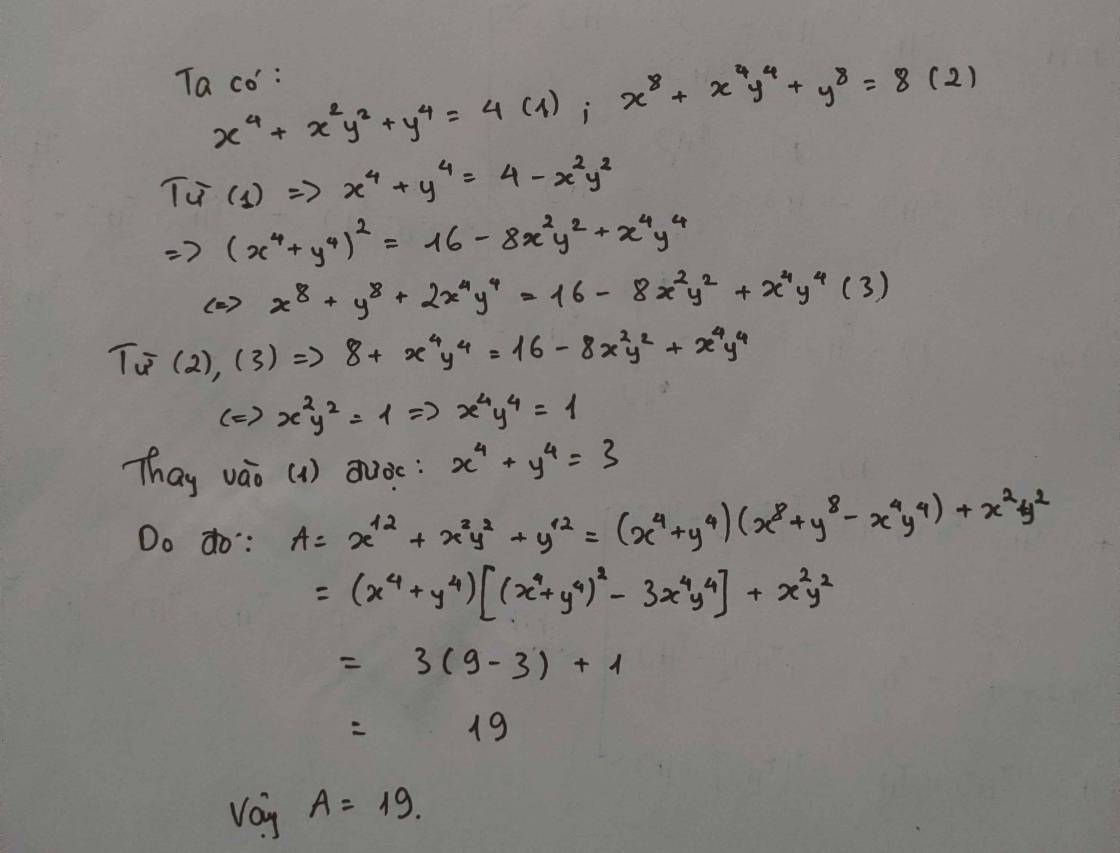Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(P=\left(x-y\right)\left(x^2+y^2\right)\left(x^4+y^4\right)-x^8+y^8+1\)
\(\Leftrightarrow P=\left(x-y\right)\left(x+y\right)\left(x^2+y^2\right)\left(x^4+y^4\right)-x^8+y^8+1\) (Vì: \(x-y=1\))
\(\Leftrightarrow P=\left(x^2-y^2\right)\left(x^2+y^2\right)\left(x^4+y^4\right)-x^8+y^8+1\)
\(\Leftrightarrow P=\left(x^4-y^4\right)\left(x^4+y^4\right)-x^8+y^8+1\)
\(\Leftrightarrow P=x^8-y^8-x^8+y^8+1\)
\(\Leftrightarrow P=1\)

Từ x8+x4y4+y8=(x4+y4)2-x4y4=(x4+y4-x2y2) (x4+y4+x2y2)=4(x4+y4-x2y2) =8
=>(x4+y4-x2y2)=2=>x4+y4=2+x2y2 kết hợp với x4+y4+x2y2=4
=> 2+x2y2+x2y2=4 => x2y2=1 (x4y4 sẽ = 1 nốt ) => x4+y4=3 và x8+y8=7
Xét (x4+y4)3=x12+y12+3x4y4(x4+y4)=x12+y12+3.1.3=33=27
=>x12+y12=18=> A = 18+1=19

Bài làm:
a) \(\left(x^4-2x^2y+y^2\right)\div\left(y-x^2\right)\)
\(=\left(x^2-y\right)^2\div\left(y-x^2\right)\)
\(=\left(y-x^2\right)^2\div\left(y-x^2\right)\)
\(=y-x^2\)
b) \(\left(x^2-2xy^2+y^4\right)\div\left(x-y^2\right)\)
\(=\left(x-y^2\right)^2\div\left(x-y^2\right)\)
\(=x-y^2\)

Ta có:
\(\frac{x^4}{a}+\frac{y^4}{b}\ge\frac{\left(x^2+y^2\right)^2}{a+b}=\frac{1}{a+b}\)
Dấu = xảy ra khi .... Làm tiếp nhé
ta có: \(\frac{x^4}{a}+\frac{y^4}{b}=\frac{1}{a+b}\)=> \(\frac{bx^4+ay^4}{ab}=\frac{\left(x^2+y^2\right)^2}{a+b}\) (vì x^2 +y^2 =1)
=>\(abx^4+b^2x^4+aby^4+a^2y^4\) = \(ab\left(x^4+2x^2y^2+y^4\right)\)
=>\(abx^4+b^2x^4+aby^4+a^2y^4\) = \(abx^4+2abx^2y^2+aby^4\)
=> \(b^2x^4-2abx^2y^2+a^2y^4=0\)
=>\(\left(bx^2-ay^2\right)^2=0\)=>\(bx^2=ay^2\Rightarrow\frac{x^2}{a}=\frac{y^2}{b}=\frac{x^2+y^2}{a+b}=\frac{1}{a+b}\)
=> \(\frac{x^{2012}}{a^{1006}}=\frac{1}{\left(a+b\right)^{1006}}\) và \(\frac{y^{2012}}{b^{1006}}=\frac{1}{\left(a+b\right)^{1006}}\)
=>\(\frac{x^{2012}}{a^{1006}}+\frac{y^{2012}}{b^{1006}}=\frac{2}{\left(a+b\right)^{1006}}\)

Thay x=-8 và y=6 cào C ta được:
\(C=\dfrac{\left(-8\right)^3}{2}+\dfrac{\left(-8\right)^2.6}{4}+\dfrac{\left(-8\right).6^2}{6}+\dfrac{6^3}{27}\)\(=\dfrac{-512}{2}+\dfrac{384}{4}-\dfrac{288}{6}+\dfrac{216}{27}\)\(=-256+96-48+8=-200\)

Bài 2:
a: \(A=\left(x+1\right)^3+5=20^3+5=8005\)
b: \(B=\left(x-1\right)^3+1=10^3+1=1001\)

\(.\)M= bn ghi lại đề nha ^.^
\(=\left(a+b\right)^3-3ab\left(a+b\right)+3ab\left[\left(a^2+2ab+b^2\right)-2ab\right]+6a^2b^2\left(a+b\right)\)
\(=1^3-3ab.1+3ab\left[\left(a+b\right)^2-2ab\right]+6a^2b^2.1\)
\(=1-3ab+3ab\left(1-2ab\right)+6a^2b^2\)
\(M=1-3ab+3ab-6a^2b^2+6a^2b^2\)\(=1\)
k cho mình nha bn thanks nhìu <3 <3 (^3^)
2. \(\left(x+1\right)\left(x+2\right)\left(x+3\right)\left(x+4\right)-24\)
\(=\left(x^2+5x+4\right)\left(x^2+5x+6\right)-24\)(1)
Đặt \(x^2+5x+4=t\)
(1) = \(t.\left(t+2\right)-24\)
\(=t^2+2t+1-25\)
\(=\left(t+1\right)^2-25\)
\(=\left(t+1-5\right)\left(t+1+5\right)\)
\(=\left(t-4\right)\left(t+6\right)\)(2)
Thay \(t=x^2+5x+4\)vào (2) ta có:
(2) = \(\left(x^2+5x+4-4\right)\left(x^2+5x+4+6\right)\)
\(=\left(x^2+5x\right)\left(x^2+5x+10\right)\)\(=x\left(x+5\right)\left(x^2+5x+10\right)\)
k mình nha bn <3 thanks