
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
KN
1

Các câu hỏi dưới đây có thể giống với câu hỏi trên
I
0


26 tháng 11 2017
bn gõ bài trong công thức trực quan ik, khó nhìn lắm, ko làm đc
LA
26 tháng 11 2017
1). x2y2(y-x)+y2z2(z-y)-z2x2(z-x)
2)xyz-(xy+yz+xz)+(x+y+z)-1
3)yz(y+z)+xz(z-x)-xy(x+y)
5)y(x-2z)2+8xyz+x(y-2z)2-2z(x+y)2
6)8x3(y+z)-y3(z+2x)-z3(2x-y)
7) (x2+y2)3+(z2-x2)3-(y2+z2)3
PB
0

NT
0

PK
0

DT
0


NV
Nguyễn Việt Lâm
Giáo viên
26 tháng 12 2022
\(x^2+y^2=\left(x+y\right)^2-2xy=6\)
\(x^3+y^3=\left(x+y\right)^3-3xy.\left(x+y\right)=14\)
\(x^4+y^4=\left(x^2+y^2\right)^2-2\left(xy\right)^2=34\)
\(\Rightarrow x^7+y^7=\left(x^3+y^3\right)\left(x^4+y^4\right)-\left(xy\right)^3\left(x+y\right)=478\)
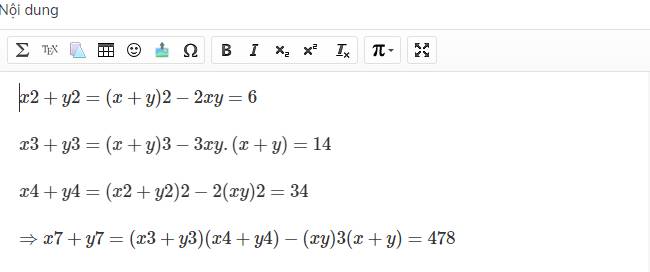
Ta có:
\(x+y+z=0\)
\(\Rightarrow x+y=-z\)
Ta lại có:
\(x^7+y^7\)
\(=\left(x^3+y^3\right)\left(x^4+y^4\right)-x^4y^x-x^3y^4\)
\(=\left(x^3+y^3\right)\left(x^4+y^4\right)-x^3y^3\left(x+y\right)\)
\(=\left(x^3+y^3\right)\left(x^4+y^4\right)+x^3y^3z\) ( Thay x + y = -z )
Ta sẽ đi tính \(x^3+y^4;x^4+y^4\)
Lại có:
1/ \(x^3+y^3=\left(x+y\right)^3-3xy\left(x+y\right)=-z^3+3xyz\)
2/ \(x^2+y^2=\left(x+y\right)^2-2xy=z^2-2xy\)
\(\Rightarrow x^4+y^4=\left(x^2+y^2\right)^2-2x^2y^2=\left(z^2-2xy\right)^2-2x^2y^2=z^4-4xyz^2+2x^2y^2\)
Như vậy \(x^7+y^7=\left(-z^3+3xyz\right)\left(z^4-4xyz^2+2x^2y^2\right)+x^3y^3z\)
\(\Rightarrow x^7+y^7=-z^7+7xyz^5-14x^2y^2z^3+7x^3y^3z\)
\(\Rightarrow x^7+y^7+z^7=7xyz^5-14x^2y^2z^3+7x^3y^3z\)
\(\Rightarrow x^7+y^7+z^7=7xyz\left(z^4-2xyz^2+x^2y^2\right)\)
\(\Rightarrow x^7+y^7+z^7=7xyz\left[z^2\left(z^2-2xy\right)+x^2y^2\right]\)
Mà \(z^2-2xy=x^2+y^2\)
\(\Rightarrow x^7+y^7+z^7=7xyz\left[z^2\left(x^2+y^2\right)+x^2y^2\right]\)
\(\Rightarrow x^7+y^7+z^7=7xyz\left(x^2z^2+y^2z^2+x^2y^2\right)\)