Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Cho biết x và y là hai đại lượng tỉ lệ thuận với nhau.
a) Biết rằng hiệu hai giá trị nào đó của x là 6 và hiệu hai giá trị tương ứng của y là -3. Hỏi hai đại lượng x và y liên hệ với nhau bởi công thức nào?
b) Từ đó hãy điền tiếp số thích hợp vào ô trống trong bảng sau:

a: x và y tỉ lệ thuận nên \(\dfrac{x_1}{y_1}=\dfrac{x_2}{y_2}\)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x_1}{y_1}=\dfrac{x_2}{y_2}=\dfrac{x_1+x_2}{y_1+y_2}=\dfrac{6}{-2}=-3\)
=>x=-3y
b: x=-3y
=>\(y=-\dfrac{1}{3}x\)
Thay x=2 vào \(y=-\dfrac{1}{3}x\), ta được:
\(y=-\dfrac{1}{3}\cdot2=-\dfrac{2}{3}\)
Thay x=4 vào \(y=-\dfrac{1}{3}x\), ta được:
\(y=-\dfrac{1}{3}\cdot4=-\dfrac{4}{3}\)

Vì x và y là hai đại lượng tỉ lệ thuận nên ta có:
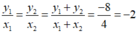
Vậy y tỉ lệ với x theo hệ số tỉ lệ là – 2 : y = -2x
Với x = -2 thì y = (-2). (-2) = 4
Chọn đáp án D

a: x và y là hai đại lượng tỉ lệ thuận
=>\(\dfrac{x_1}{y_1}=\dfrac{x_2}{y_2}\)
mà \(x_1+x_2=2;y_1+y_2=10\)
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x_1}{y_1}=\dfrac{x_2}{y_2}=\dfrac{x_1+x_2}{y_1+y_2}=\dfrac{2}{10}=\dfrac{1}{5}\)
=>\(\dfrac{x}{y}=\dfrac{1}{5}\)
=>y=5x
b: Khi x=1 thì \(y=5\cdot1=5\)

Vì x và y là hai đại lượng tỉ lệ thuận, nên:
y = ax (a là hệ số tỉ lệ, a khác 0)
Khi đó: y1 = a.x1 và y2 = a.x2
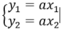
Suy ra y1 + y2 = ax1 + ax2 = a(x1 + x2)
Vậy : y = -5x.
Ta có \(\dfrac{x_1}{y_1}=\dfrac{x_2}{y_2}=\dfrac{x_1+x_1}{y_1+y_2}=\dfrac{15}{20}=\dfrac{3}{4}\)
\(\Rightarrow\left\{{}\begin{matrix}y_1=\dfrac{4}{3}x_1\\y_2=\dfrac{4}{3}x_2\end{matrix}\right.\Rightarrow y=\dfrac{4}{3}x\)
Với \(x=1,5=\dfrac{3}{2}\Rightarrow y=\dfrac{4}{3}\cdot\dfrac{3}{2}=2\)
tích cho mik nha
=))