Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

x và y tỉ lệ nghịch
=>x1y1=x2y2
=>y1/x2=y2/x1
=>y1/5,6=y2/3,4=(5y1-3y2)/(5*5,6-3*3,4)=35,6/17,8=2
=>y1=11,2; y2=6,8

Lời giải:
Vì $x,y$ tỉ lệ nghịch nên đặt $xy=k$ với $k\in\mathbb{R}$. Ta có:
$x_1y_1=k=x_2y_2$
$\Leftrightarrow 8x_1=-12x_2$
$\Leftrightarrow x_1=-1,5x_2$
Thay vô $x_1-5x_2=-39$ thì:
$-1,5x_2-5x_2=-39\Leftrightarrow -6,5x_2=-39$
$\Rightarrow x_2=6$
$x_1=-1,5x_2=-9$
b.
$xy=x_1y_1=(-9).8=-72$
$\Rightarrow y=\frac{-72}{x}$

Với x và y là hai đại lượng tỉ lệ nghịch nên x 1 y 1 = x 2 y 2 mà x 1 = 4 , x 2 = 3 và y 1 + y 2 = 14
Do đó: 4 y 1 = 3 y 2 ⇒ y 1 3 = y 2 4
Áp dụng tính chất của dãy tỉ số bằng nhau ta được:
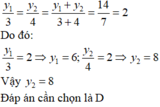

Vì x và y là hai đại lượng tỉ lệ nghịch nên x 1 y 1 = x 2 y 2 m à x 1 = 4 ; x 2 = 3 v à y 1 + y 2 = 14
Do đó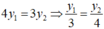
Áp dụng tính chất của dãy tỉ số bằng nhau ta có:
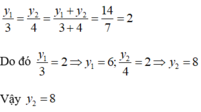
Chọn đáp án D

a) x và y là hai đại lượng tỷ lệ thuận
nên x1/y1 = x2/y2
suy ra x1=x2.y1/y2 = 2.(-3/4):1/7 =-21/2
b) x và y là hai đại lượng tỷ lệ thuận
nên x1/y1 = x2/y2
<=> x1/x2 = y1/y2 = (y1-x1)/(y2-x2) (theo t/c của dãy tỷ số bằng nhau)
Thay số ta có:
x1/(-4) = y1/3=-2/(3-(-4))
<=> x1/(-4) = y1/3=-2/7
suy ra:
x1 = (-4).(-2/7)=8/7
y1 = 3.(-2/7)=-6/7
k nha mk trả lời đầu tiên đó!!!
Chúc bn thành công

Với x và y là hai đại lượng tỉ lệ nghịch nên x 1 y 1 = x 2 y 2 mà x 2 = − 4 ; y 1 = − 10 và 3 x 1 - 2 y 2 = 32
Nên ta có:
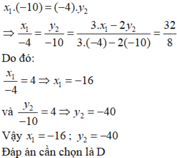

Vì \(x\) và \(y\) là hai đại tượng tỉ lệ nghịch nên \(xy=a\left(a\ne0\right)\)
Thay các giá trị tương ứng của \(x\) và \(y\) ta được :
\(x_1.y_1=x_2.y_2\)
\(\Rightarrow\dfrac{y_1}{x_2}=\dfrac{y_2}{x_1}\)
\(\Rightarrow\dfrac{y_1}{3}=\dfrac{y_2}{4}\)
- Áp dụng t/c dãy tỉ số bằng nhau, ta có :
\(\dfrac{y_1}{3}=\dfrac{y_2}{4}=\dfrac{y_1+y_2}{3+4}=\dfrac{14}{7}=2\)
\(\Rightarrow y_2=2.4=8\)
Lời giải:
Đặt $xy=k$
$\Rightarrow x_1y_1=k=x_2y_2$. Ta có:
$-3y_1=k; 5x_2=k$
$\Rightarrow -3y_1=5x_2$. Thay vào $5x_2-3y_1=-60$ thì:
$-3y_1-3y_1=-60$
$-6y_1=-60$
$y_1=10$
$x_2=\frac{-3y_1}{5}=\frac{-3.10}{5}=-6$
Vậy $y_1=10; x_2=-6$
$k=x_1y_1=-3.10=-30$
Vậy $xy=-30$