Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Ta có: Om là phân giác của góc xOz
=>\(\widehat{xOm}=\widehat{zOm}=\dfrac{1}{2}\cdot\widehat{xOz}\)
Ta có: \(\widehat{xOz}+\widehat{yOz}=180^0\)(hai góc kề bù)
=>\(2\cdot\widehat{zOm}+\widehat{yOz}=2\left(\widehat{zOm}+\widehat{zOn}\right)\)
=>\(\widehat{yOz}=2\cdot\widehat{zOm}+2\cdot\widehat{zOn}-2\cdot\widehat{zOm}=2\cdot\widehat{zOn}\)
=>On là phân giác của góc yOz
b: Ta có: At//Oz
=>\(\widehat{tAy}=\widehat{zOy}\)(hai góc đồng vị)
mà \(\widehat{yAu}=\dfrac{\widehat{yAt}}{2}\)(Au là phân giác của góc yAt)
và \(\widehat{yOn}=\dfrac{\widehat{yOz}}{2}\)(On là phân giác của góc yOz)
nên \(\widehat{yAu}=\widehat{yOn}\)
mà hai góc này là hai góc ở vị trí đồng vị
nên Au//On
mà On\(\perp\)Om
nên Au\(\perp\)Om

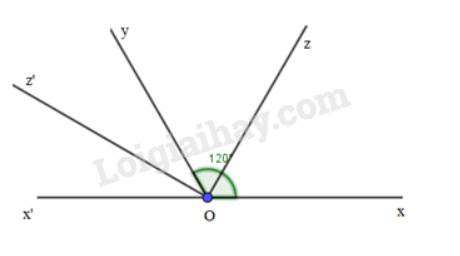
Vì Oz là tia phân giác của \(\widehat {xOy}\) nên \(\widehat {xOz} = \widehat {zOy} = \frac{1}{2}.\widehat {xOy} = \frac{1}{2}.120^\circ = 60^\circ \)
Vì Oz’ là tia phân giác của \(\widehat {yOx'}\) nên \(\widehat {x'Oz'} = \widehat {yOz'} = \frac{1}{2}.\widehat {yOx'} = \frac{1}{2}.60^\circ = 30^\circ \)
Vì tia Oy nằm trong \(\widehat {zOz'}\) nên \(\widehat {zOz'}=\widehat {zOy} + \widehat {yOz'} = 60^\circ + 30^\circ = 90^\circ \)
Vậy \(\widehat {zOy} = 60^\circ ,\widehat {yOz'} = 30^\circ ,\widehat {zOz'} = 90^\circ \)
Chú ý:
2 tia phân giác của 2 góc kề bù thì vuông góc với nhau

`Answer:`
Ta có `hat{zOt}+\hat{yOz}=90^o`
\(\Rightarrow\frac{1}{2}.Oz+\widehat{yOz}=90^o\)
\(\Rightarrow\frac{1}{2}.4\widehat{yOz}+\widehat{yOz}=90^o\)
\(\Rightarrow\widehat{yOz}.3=90^o\)
\(\Rightarrow\widehat{yOz}=30^o\)
`=>\hat{xOz}=120^o` (Vì `\hat{xOz}=4\hat{yOz}`
Vậy `\hat{xOy}=\hat{yOz}+\hat{xOz}=120^o+30^o=150^o`

(Bạn tự vẽ hình nha)
Vì xOy và yOz là hai góc kề bù
=> Tia Oy nằm giữa ai tia Ox và Oz(1)
xOy + yOz = 180o
Vì Oa là tia phân giác của xOy
=> Tia Oa nằm giữa 2 tia Ox và Oy(2)
xOa = aOy = 1/2 xOy
Vì Ob là tia phân giác của yOz
=> Tia Ob nằm giữa hai tia Oy và Oz(3)
yOb = bOz = 1/2 yOz
Từ (1); (2) và (3) => Tia Oy nằm giữa hai tia Oa và Ob
=> aOb = aOy + yOb =\(\frac{1}{2}\widehat{xOy}+\frac{1}{2}\widehat{yOz}=\frac{1}{2}\left(\widehat{xOy}+\widehat{yOz}\right)=\frac{1}{2}\times180^o=90^o\)
=> Oa vuông góc với Ob (đpcm)

Om là phân giác góc xOy
=> góc mOy = 1/2 góc xOy
On là phân giác góc yOz
=> góc yOn = 1/2 góc yoz
suy ra: góc mOy + góc yOn = 1/2 (góc xOy + góc yOz)
<=> góc mOn = 1/2.1800 = 900 (do góc xOy và góc yOz kề bù)
Om phân giác xoy => moy=1/2xoy hay xoy=2moy
tương tự => noy=1/2yoz hay yoz=2noy
Lại có:
xoy+yoz=180
=>2moy +2noy=180
=>moy+noy=90 hay mon =90

\(\widehat{aOy}=\dfrac{\widehat{xOy}}{2}\)
\(\widehat{bOy}=\dfrac{\widehat{zOy}}{2}\)
Do đó: \(\widehat{aOy}+\widehat{bOy}=\dfrac{1}{2}\left(\widehat{xOy}+\widehat{yOz}\right)=\dfrac{1}{2}\cdot180^0\)
hay \(\widehat{aOb}=90^0\)(đpcm)

Ta có góc xoy+yoz=180 độ (kề bù)
=> 1/2 góc xoy+1/2 góc yoz = 90 độ
=> góc yom + góc yon=90 độ
=> góc mon =90 độ hay om vuông góc với on

