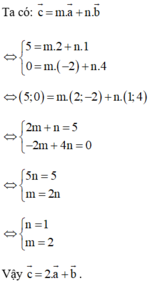Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Câu 4:
Áp dụng định lý Pytago
\(BC^2=AB^2+AC^2\Rightarrow BC=2\)
Ta có:
\(\overrightarrow{CA}.\overrightarrow{BC}=-\overrightarrow{CA}.\overrightarrow{CB}=-\dfrac{CA^2+CB^2-AB^2}{2}=-\dfrac{2+4-2}{2}=-2\)
Câu 5:
Gọi M là trung điểm BC
\(\overrightarrow{AM}=\dfrac{1}{2}\left(\overrightarrow{AB}+\overrightarrow{AC}\right)\)
Mà: \(\overrightarrow{AG}=\dfrac{2}{3}\overrightarrow{AM}=\dfrac{1}{3}\left(\overrightarrow{AB}+\overrightarrow{AC}\right)\)
Câu 6:
\(\left|\overrightarrow{a}-\overrightarrow{b}\right|=3\)
\(a^2+b^2-2\overrightarrow{a}.\overrightarrow{b}=9\)
\(\overrightarrow{a}.\overrightarrow{b}=\dfrac{1^2+2^2-9}{2}=-2\)
Câu 7:
\(\left|\overrightarrow{AB}-\overrightarrow{AD}+\overrightarrow{CD}\right|=\left|\overrightarrow{DB}+\overrightarrow{CD}\right|\)
\(=\left|\overrightarrow{DB}-\overrightarrow{DC}\right|=\left|\overrightarrow{CB}\right|=BC=a\)

Lời giải:
Để $\overrightarrow{a}$ và $\overrightarrow{b}$ cùng phương thì:
\(\frac{2}{5}=\frac{-3}{m}\Rightarrow m=\frac{-15}{2}\)
Đáp án D.

a) Ta có:
\(\overrightarrow{AM}=\overrightarrow{AB}+\overrightarrow{BM}\)
\(=\overrightarrow{AB}+k\overrightarrow{BC}\)
\(=\overrightarrow{AB}+k\left(\overrightarrow{AC}-\overrightarrow{AB}\right)\)
\(=\left(1-k\right)\overrightarrow{AB}+k\overrightarrow{AC}\)
b) \(\overrightarrow{NP}=\overrightarrow{AP}-\overrightarrow{AN}\)
\(=\dfrac{2}{3}\overrightarrow{AC}-\dfrac{3}{4}\overrightarrow{AB}\)
Để \(AM\perp NP\)
\(\Rightarrow\overrightarrow{AM}.\overrightarrow{NP}=\overrightarrow{0}\)
\(\Rightarrow\left[\left(1-k\right)\overrightarrow{AB}+k\overrightarrow{AC}\right]\left(-\dfrac{3}{4}\overrightarrow{AB}+\dfrac{2}{3}\overrightarrow{AC}\right)=\overrightarrow{0}\)
\(\Leftrightarrow\dfrac{3\left(k-1\right)}{4}AB^2+\dfrac{2k}{3}AC^2+\dfrac{2\left(1-k\right)}{3}\overrightarrow{AB}.\overrightarrow{AC}-\dfrac{3k}{4}\overrightarrow{AB}.\overrightarrow{AC}=\overrightarrow{0}\)
\(\Leftrightarrow\dfrac{3\left(k-1\right)}{4}AB^2+\dfrac{2k}{3}AB^2+\dfrac{1-k}{3}AB^2-\dfrac{3k}{8}AB^2=0\)
\(\Leftrightarrow AB^2\left[\dfrac{3\left(k-1\right)}{4}+\dfrac{2k}{3}+\dfrac{1-k}{3}-\dfrac{3k}{8}\right]=0\)
\(\Leftrightarrow18\left(k-1\right)+16k+8\left(1-k\right)-9k=0\left(AB>0\right)\)
\(\Leftrightarrow17k=10\)
\(\Leftrightarrow k=\dfrac{10}{17}\)

Gọi \(M\left(m;0\right)\Rightarrow\left\{{}\begin{matrix}\overrightarrow{MA}=\left(1-m;1\right)\\\overrightarrow{MB}=\left(-2-m;4\right)\end{matrix}\right.\)
\(\Rightarrow\overrightarrow{MA}-2\overrightarrow{MB}=\left(m+5;-7\right)\)
\(\Rightarrow\left|\overrightarrow{MA}-2\overrightarrow{MB}\right|=\sqrt{\left(m+5\right)^2+49}\ge7\)
Dấu "=" xảy ra khi \(m+5=0\Leftrightarrow m=-5\) hay \(M\left(-5;0\right)\)