Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a)hình bạn tự vẽ nha chứ mik vẽ lâu lắm
b)ta có:
\(\Delta\)OAB đồng dạng với \(\Delta\)OA'B':
\(\Rightarrow\dfrac{OA}{OA'}=\dfrac{AB}{A'B'}\)
\(\Delta\)OIF' đồng dạng với \(\Delta\)A'B'F'
\(\Rightarrow\dfrac{OI}{A'B'}=\dfrac{OF'}{A'F'}\)
\(\Leftrightarrow\dfrac{AB}{A'B'}=\dfrac{OF'}{OA'-OF'}\)
\(\Leftrightarrow\dfrac{OA}{OA'}=\dfrac{OF'}{OA'-OF'}\)
\(\Leftrightarrow OA.OA'-OA.OF'=OF'.OA'\)
chia hai về cho OA.OA'.OF'
\(\Rightarrow\dfrac{1}{OF}-\dfrac{1}{OA'}=\dfrac{1}{OA}\)
mà OA=2OF'\(\Rightarrow OF'=0,5OA\)
\(\Rightarrow\dfrac{1}{0,5OA}-\dfrac{1}{OA'}=\dfrac{1}{OA}\)
\(\Leftrightarrow\dfrac{1}{0,5OA}-\dfrac{1}{OA}=\dfrac{1}{OA'}\)
\(\Leftrightarrow\dfrac{2}{OA}-\dfrac{1}{OA}=\dfrac{1}{OA'}\)
\(\Leftrightarrow\dfrac{1}{OA}=\dfrac{1}{OA'}\Rightarrow OA=OA'\)
c)ta có:
\(\dfrac{OA}{OA'}=\dfrac{AB}{A'B'}\)
\(\Leftrightarrow\dfrac{h}{h'}=\dfrac{OA}{OA'}\)
mà OA=OA' nên:
\(\dfrac{h}{h'}=1\Rightarrow h=h'\)
d)ta có:
\(\dfrac{1}{OF'}=\dfrac{1}{OA'}+\dfrac{1}{OA}\)
mà OA=OA' nên:
\(\dfrac{1}{f}=\dfrac{2}{OA}\)
\(\Rightarrow f=\dfrac{OA}{2}=\dfrac{OA'}{2}\)

Để có được ảnh rõ nét trên màn tức là di chuyển đến TK đến vị trí mà màn chắn hứng được ảnh thật của vật.
Ta có 2 vị trí có thể cho ảnh rõ nét là khi vật cách TK 1 đoạn d hoặc d'=L-d sao cho thỏa mãn: \(\dfrac{1}{d}+\dfrac{1}{d'}=\dfrac{1}{f}\)
Từ công thức suy ra : \(f\left(d+d'\right)=d.d'\)
Giả sử d>d. Ta có: L=d+d' và l=d-d'
=> \(L^2-l^2=\left(d+d'\right)^2-\left(d-d'\right)^2=4d.d'\left(1\right)\)
và : \(4Lf=4\left(d+d'\right)f=4d.d'\left(2\right)\)
Từ (1) và (2) => \(L^2-l^2=4Lf.\)
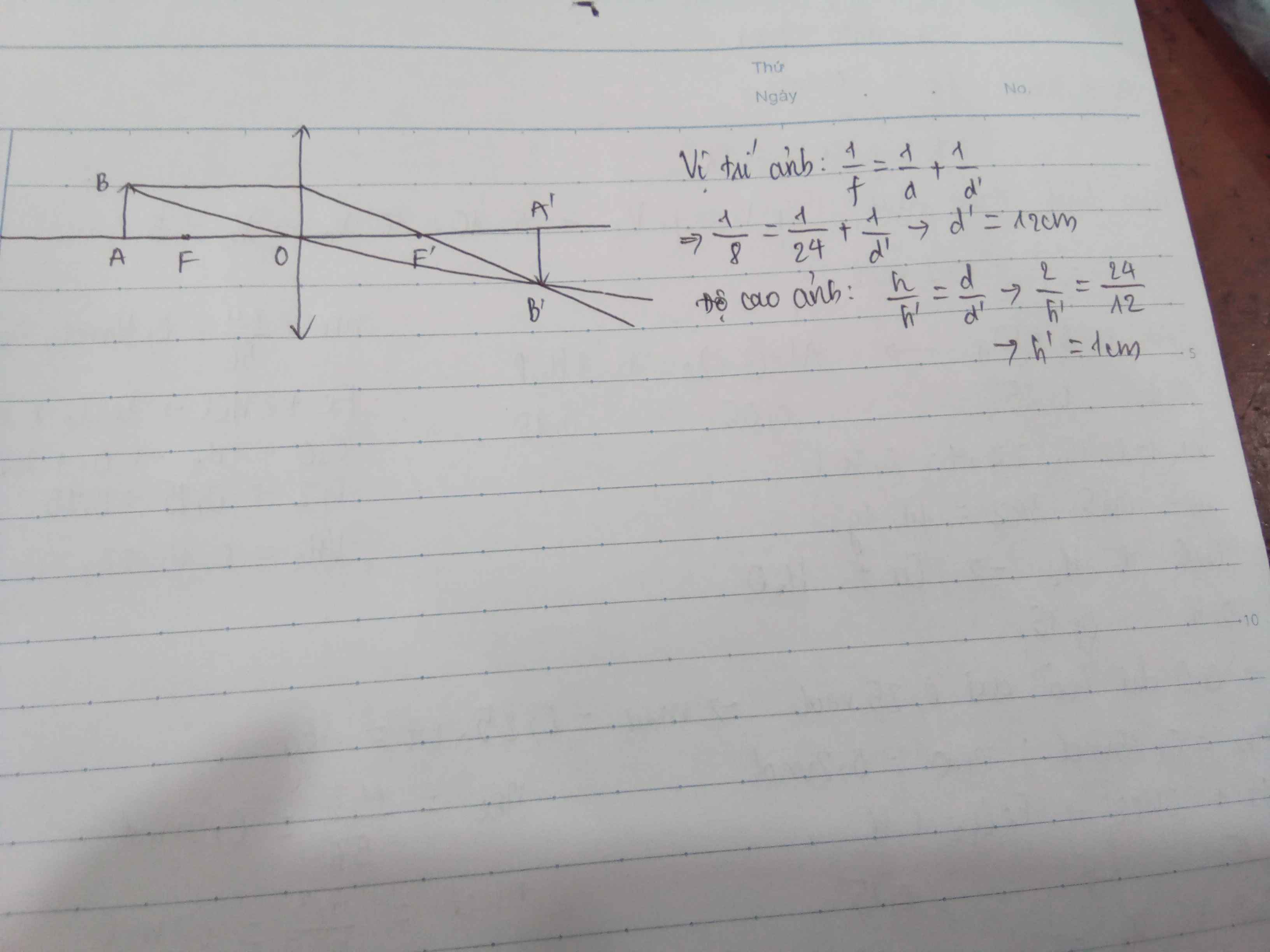

a)
b) Ta có ΔBOA∼ΔB'OA'
=>\(\dfrac{BA}{AO}=\dfrac{B'A'}{OA'}\)
=>\(\dfrac{h}{d}=\dfrac{h'}{d'}\Rightarrow\dfrac{h}{h'}=\dfrac{d}{d'}\) (1)
Lại có ΔIOF'∼ΔB'A'F'
=>\(\dfrac{IO}{A'B'}=\dfrac{OF'}{A'F'}\)
mà IO=AB=h
A'F'=A'O-OF'=d'-f'
=>\(\dfrac{h}{h'}=\dfrac{f}{d'-f'}\) (2)
Từ (1) và (2)
=>\(\dfrac{d}{d'}=\dfrac{f}{d'-f'}\)
=>dd'-df'=d'f
Chia mỗi vế cho dd'f
(f=f ')
=>\(\dfrac{1}{f}-\dfrac{1}{d'}=\dfrac{1}{d}\)
=>\(\dfrac{1}{f}=\dfrac{1}{d}+\dfrac{1}{d'}\)
đpcm
đ? nào nằm trên trục chính??
A hay B ??