Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

* Hướng dẫn câu b:
Gọi I là giao điểm của Gx và PQ. Kéo dài PQ cắt hai cạnh AD và BC theo thứ tự là E và F.
Góc MPQ = góc GEF (so le trong do MP // AD)
Góc MQP = góc GFE (so le trong do MQ // BC)
góc MPQ = góc MQP (tam giác MPQ cân do MP = MQ)
=> góc GEF = góc GEF -> tam giác GEF cân tại G
mà GI là phân giác của góc G -> GI vuông góc với EF
-> Gx vuông góc với PQ -> Gx // MN (MN vuông góc với PQ do hình thoi có 2 đường chéo vuông góc).
Ta có thể tìm các bội của một số khác 0 bằng cách nhân số đó lần lược cho 1, 2, 3, …
Ví dụ :
B(5) = {5.1, 4.2, 5.3, …} = {5, 10, 15, …}
Ta có thể tìm các ước của một số a (a > 1) bằng cách lần lược chia số a cho số tự nhiên từ 1 đến a để xét xem a chia hết cho những số nào, khi đó các số ấy là ước của a.

a: Xét ΔABD có
E là trung điểm của AB
H là trung điểm của AD
Do đó: EH là đường trung bình của ΔABD
Suy ra: EH//BD và \(EH=\dfrac{BD}{2}\left(1\right)\)
Xét ΔBCD có
F là trung điểm của BC
G là trung điểm của DC
Do đó: FG là đường trung bình của ΔBCD
Suy ra: FG//BD và \(FG=\dfrac{BD}{2}\left(2\right)\)
Từ (1) và (2) suy ra EH//GF và EH=GF
hay EHGF là hình bình hành

Bài 1:
a: Xét tứ giác AMCN có
AM//CN
AM=CN
Do đó: AMCN là hình bình hành
b: Ta có: AD⊥AC
mà AD//BC
nên BC⊥CA
=>ΔCBA vuông tại C
mà CM là đường trung tuyến
nên CM=MA
=>ΔMCA cân tại M
=>\(\widehat{MAC}=\widehat{MCA}\)
mà \(\widehat{MAC}=\widehat{DCA}\)
nên \(\widehat{MCA}=\widehat{DCA}\)
hay CA là tia phân giác của góc MCD

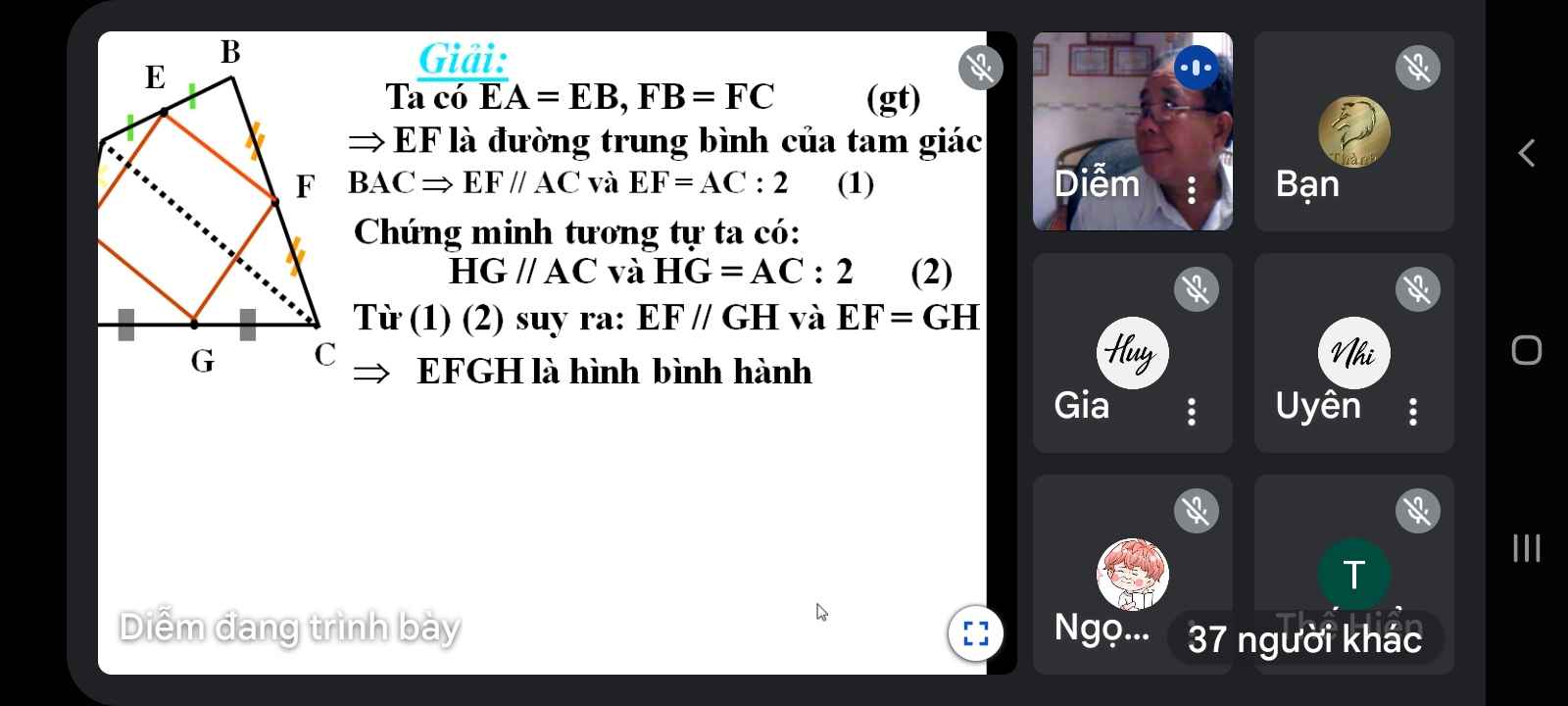
a) Xét ΔABC có
E là trung điểm của AB(gt)
F là trung điểm của BC(gt)
Do đó: EF là đường trung bình của ΔABC(Định nghĩa đường trung bình của tam giác)
⇒EF//AC và \(EF=\dfrac{AC}{2}\)(Định lí 2 về đường trung bình của tam giác)(1)
Xét ΔADC có
H là trung điểm của AD(gt)
G là trung điểm của CD(gt)
Do đó: HG là đường trung bình của ΔADC(Định nghĩa đường trung bình của tam giác)
⇒HG//AC và \(HG=\dfrac{AC}{2}\)(Định lí 2 về đường trung bình của tam giác)(2)
Từ (1) và (2) suy ra HG//EF và HG=EF
Xét ΔABD có
E là trung điểm của AB(gt)
H là trung điểm của AD(gt)
Do đó: EH là đường trung bình của ΔABD(Định nghĩa đường trung bình của tam giác)
⇒EH//BD và \(EH=\dfrac{BD}{2}\)(Định lí 2 về đường trung bình của tam giác)
Ta có: EH//BD(cmt)
BD⊥AC(gt)
Do đó: EH⊥AC(Định lí 2 từ vuông góc tới song song)
Ta có: HG//AC(cmt)
EH⊥AC(Cmt)
Do đó: HG⊥HE(Định lí 2 từ vuông góc tới song song)
hay \(\widehat{EHG}=90^0\)
Xét tứ giác EHGF có
HG//EF(cmt)
HG=FE(cmt)
Do đó: EHGF là hình bình hành(Dấu hiệu nhận biết hình bình hành)
Hình bình hành EHGF có \(\widehat{EHG}=90^0\)(cmt)
nên EHGF là hình chữ nhật(Dấu hiệu nhận biết hình chữ nhật)
b) Ta có: EFGH là hình chữ nhật(cmt)
nên \(S_{EFGH}=EF\cdot EH\)
\(\Leftrightarrow S_{EFGH}=\dfrac{AC}{2}\cdot\dfrac{BD}{2}=\dfrac{10}{2}\cdot\dfrac{8}{2}=5\cdot4=20cm^2\)
Vậy: Diện tích tứ giác EFGH khi AC=10cm và BD=8cm là 20cm2
c) Hình chữ nhật EFGH trở thành hình vuông khi EH=HG
hay AC=BD
Vậy: Khi tứ giác ABCD có thêm điều kiện AC=BD thì EFGH trở thành hình vuông
CHTT nha bạn !
là sao?