Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi giao điểm của FI với BC là M . Góc EMF là góc ngoài đỉnh F của hai tam giác MBF và MIE , ta có :
\(\widehat{EMF}\)\(=\widehat{F_1}\)\(+\widehat{MBF}\)
\(\widehat{EMF}\)\(=\widehat{F_2}\)\(+\widehat{EIF}\)
Suy ra : \(\widehat{EIF}\)\(+\widehat{F_2}\)\(=\widehat{F_1}\)\(+\widehat{MBF}\)\(\left(1\right)\)
Gọi giao điểm của EI với CD là N
Chứng minh tương tự , ta có :
\(\widehat{EIF}\)\(+\widehat{F_2}\)\(=\widehat{NDF}\)\(+\widehat{E_1}\)\(\left(2\right)\)\(...\)

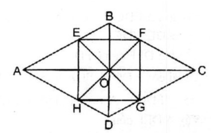
Ta có: ∠ (AOB) và ∠ (COD) đối đỉnh nên E, O, G thẳng hàng
∠ (BOC) và ∠ (AOD) đối đỉnh nên F, O, H thẳng hàng
Xét ∆ BEO và ∆ BFO:
∠ (EBO) = ∠ (FBO) (tính chất hình thoi)
OB cạnh chung
∠ (EOB) = ∠ (FOB) = 45 0 (gt)
Do đó: ∆ BEO = ∆ BFO (g.c.g)
⇒ OE = OF (1)
Xét ∆ BEO và ∆ DGO:
∠ (EBO) = ∠ (GDO) (so le trong)
OB = OD(tính chất hình thoi)
∠ (EOB) = ∠ (GOD) (đối đỉnh)
Do đó: ∆ BEO = ∆ DGO (g.c.g)
⇒ OE = OG (2)
Xét ∆ AEO và ∆ AHO:
∠ (EAO) = ∠ (HAO) (tính chất hình thoi)
OA cạnh chung
∠ (EOA) = ∠ (HOA) = 45 0 (gt)
Do đó: ∆ AEO = ∆ AHO (g.c.g)
⇒ OE = OH (3)
Từ (1), (2) và (3) suy ra: OE = OF = OG = OH hay EG = FH
nên tứ giác EFGH là hình chữ nhật (vì có hai đường chéo cắt nhau tại trung điểm mỗi đường và bằng nhau)
OE ⊥ OF (tính chất tia phân giác của hai góc kề bù)
hay EG ⊥ FH
Vậy hình chữ nhật EFGH là hình vuông.
