Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Tứ giác ABCD là hình bình hành
\( \Leftrightarrow \left\{ \begin{array}{l}
AB // DC\\
AB = DC
\end{array} \right.\)
Mà \(AB // DC \Leftrightarrow \overrightarrow {AB} ,\, \overrightarrow {DC} \) cùng phương, do đó cùng hướng.
\( \Leftrightarrow \left\{ \begin{array}{l}
\overrightarrow {AB} , \overrightarrow {DC} \,{\rm{ cùng hướng}}\\
AB = DC
\end{array} \right.\)
\(\Leftrightarrow \overrightarrow {AB} = \overrightarrow {DC} \)
Vậy tứ giác ABCD là hình bình hành khi và chỉ khi \(\overrightarrow {AB} = \overrightarrow {DC} \).
Ta chứng minh hai mệnh đề:
- Khi =
thì ABCD là hình bình hành.
Thật vậy, theo định nghĩa của vec tơ bằng nhau thì:
=
⇔
=
và và
cùng hướng.
và
cùng hướng =>
và
cùng phương, suy ra giá của chúng song song với nhau, hay AB // DC (1)
Ta lại có =
=> AB = DC (2)
Từ (1) và (2), theo dấu hiệu nhận biết hình bình hành, tứ giác ABCD có một cặp cạnh song song và bằng nhau nên nó là hình bình hành.
- Khi ABCD là hình bình hành thì =
Khi ABCD là hình bình hành thì AB // CD. Dễ thấy, từ đây ta suy ra hai vec tơ và
cùng hướng (3)
Mặt khác AB = CD => =
(4)
Từ (3) và (4) suy ra =
.
Tứ giác ABCD là một hình bình hành \( \Leftrightarrow \left\{ \begin{array}{l}AD//\;BC\\AD = BC\end{array} \right.\)
\( \Leftrightarrow \) Hai vecto \(\overrightarrow {AD} \) và \(\overrightarrow {BC} \) cùng hướng và AD = BC.
\( \Leftrightarrow \overrightarrow {BC} = \overrightarrow {AD} .\) (đpcm)
a) Mệnh đề \(P \Rightarrow Q\) là: “Nếu tứ giác ABCD là hình chữ nhật thì tứ giác ABCD là hình bình hành”
Đúng vì mỗi hình chữ nhật đều là hình bình hành.
b) Mệnh đề \(P \Rightarrow Q\) là: “Nếu tứ giác ABCD là hình thoi thì tứ giác ABCD là hình vuông”
Sai vì hầu hết các hình thoi không là hình vuông
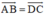
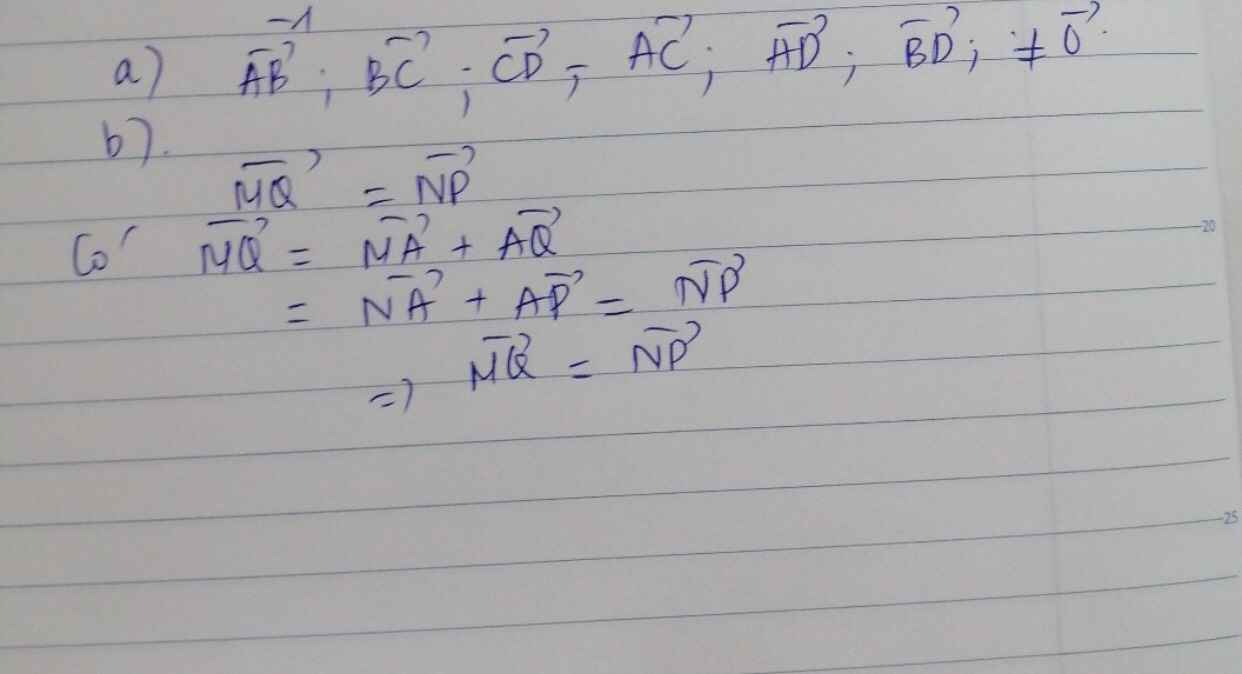
Ta chứng minh hai mệnh đề:
– Khi
= 
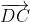thì ABCD là hình bình hành.
Thật vậy, theo định nghĩa của vec tơ bằng nhau thì:
và
và 
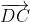cùng hướng.
Ta lại có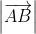
= 
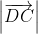=> AB = DC (2)
Từ (1) và (2), theo dấu hiệu nhận biết hình bình hành, tứ giác ABCD có một cặp cạnh song song và bằng nhau nên nó là hình bình hành.
– Khi ABCD là hình bình hành thì
= 
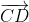
Khi ABCD là hình bình hành thì AB // CD. Dễ thấy, từ đây ta suy ra hai vec tơ
và 
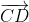cùng hướng (3)
Mặt khác AB = CD =>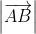
= 
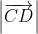(4)
Từ (3) và (4) suy ra
= 
.
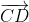bạn cho mình hỏi: nếu vecto AB = vecto AB thì làm sao cùng hướng được, có thể ngược hướng mà