Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Để tìm giao điểm của SB và mp(ABC), ta cần tìm giao điểm của hai đường thẳng SB và đường thẳng chứa điểm trung điểm I và vuông góc với mặt phẳng ABC. Vì I là trung điểm BC, ta có thể xác định được mặt phẳng ABC. Sau đó, ta tìm giao điểm của đường thẳng SB và mặt phẳng ABC.
Để tìm giao điểm của HB và mp(SAC), ta cần tìm giao điểm của hai đường thẳng HB và đường thẳng chứa điểm trung điểm I và vuông góc với mặt phẳng SAC. Tương tự như trên, ta xác định được mặt phẳng SAC và sau đó tìm giao điểm của đường thẳng HB và mặt phẳng SAC.
Để tìm giao điểm của BK và mp(SAC), ta cần tìm giao điểm của hai đường thẳng BK và đường thẳng chứa điểm trung điểm I và vuông góc với mặt phẳng SAC. Tương tự như trên, ta xác định được mặt phẳng SAC và sau đó tìm giao điểm của đường thẳng BK và mặt phẳng SAC.
Để tìm giao điểm của HK và mp(ABC), ta cần tìm giao điểm của hai đường thẳng HK và đường thẳng chứa điểm trung điểm I và vuông góc với mặt phẳng ABC. Tương tự như trên, ta xác định được mặt phẳng ABC và sau đó tìm giao điểm của đường thẳng HK và mặt phẳng ABC.

2:
a: \(B\in SB\)
\(B\in\left(ABC\right)\)
Do đó: \(B=SB\cap\left(ABC\right)\)
b: Chọn mp(SAB) có chứa BH
\(SA\subset\left(SAB\right)\)
\(SA\subset\left(SAC\right)\)
Do đó: \(\left(SAB\right)\cap\left(SAC\right)=SA\)
Gọi E là giao của BH và SA
=>E là giao điểm cần tìm
c: Chọn mp(SBC) có chứa BK
\(SC\subset\left(SBC\right)\)
\(SC\subset\left(SAC\right)\)
Do đó: \(\left(SBC\right)\cap\left(SAC\right)=SC\)
Gọi F là giao của BK với SC
=>F là giao điểm cần tìm
d: Trong mp(SAC), gọi O là giao của HK với AC
mà \(AC\subset\left(ABC\right)\)
nên \(O=HK\cap\left(ABC\right)\)

1:
a: \(S\in SA\)
\(S\in SB\subset\left(SBC\right)\)
Do đó: \(S=SA\cap\left(SBC\right)\)
b: Chọn mp(SAB) có chứa SM
\(AB\subset\left(ABC\right)\)
\(AB\subset\left(SAB\right)\)
Do đó: \(AB=\left(SAB\right)\cap\left(ABC\right)\)
\(M\in AB\)
=>SM giao AB=M
=>\(M=SM\cap\left(ABC\right)\)
c: Chọn mp(BAC) có chứa MN
\(BC\subset\left(BAC\right)\)
\(BC\subset\left(SBC\right)\)
Do đó: (BAC) giao (SBC)=BC
mà \(BC\cap MN=N\)
nên \(N=MN\cap\left(SBC\right)\)
d: Chọn mp(ABC) có chứa MN
\(AC\subset\left(SAC\right)\)
\(AC\subset\left(ABC\right)\)
Do đó: \(AC=\left(SAC\right)\cap\left(ABC\right)\)
Gọi giao của MN và AC là E
=>\(E=MN\cap\left(SAC\right)\)

a: \(BC\subset\left(SBC\right)\)
\(BC\subset\left(ABC\right)\)
Do đó: \(\left(SBC\right)\cap\left(ABC\right)=BC\)
b: \(I\in BC\subset\left(SBC\right)\)
\(I\in\left(SAI\right)\)
Do đó: \(I\in\left(SBC\right)\cap\left(SAI\right)\)
mà S thuộc (SBC) giao (SAI)
nên (SBC) giao (SAI)=SI
c: Trong mp(SBC), Gọi M là giao của BK với SI
\(M\in BK\subset\left(ABK\right)\)
\(M\in SI\subset\left(SAI\right)\)
=>\(M\in\left(SAI\right)\cap\left(ABK\right)\)
mà A thuộc (SAI) giao (ABK)
nên (SAI) giao (ABK)=AM

a: \(N\in NP\)
\(N\in\left(NMQ\right)\)
Do đó: \(N=NP\cap\left(MNQ\right)\)
b: Trong mp(PNQ), Gọi E là giao của NQ và HK
mà \(NQ\subset\left(MNQ\right)\)
nên \(E=HK\cap\left(MNQ\right)\)
c; \(K\in\left(MHK\right)\)
\(K\in QP\subset\left(NPQ\right)\)
Do đó: \(K\in\left(MHK\right)\cap\left(NPQ\right)\)
\(H\in NP\subset\left(NPQ\right)\)
\(H\in\left(MHK\right)\)
Do đó; \(H\in\left(MHK\right)\cap\left(NPQ\right)\)
=>\(\left(MHK\right)\cap\left(NPQ\right)=KH\)

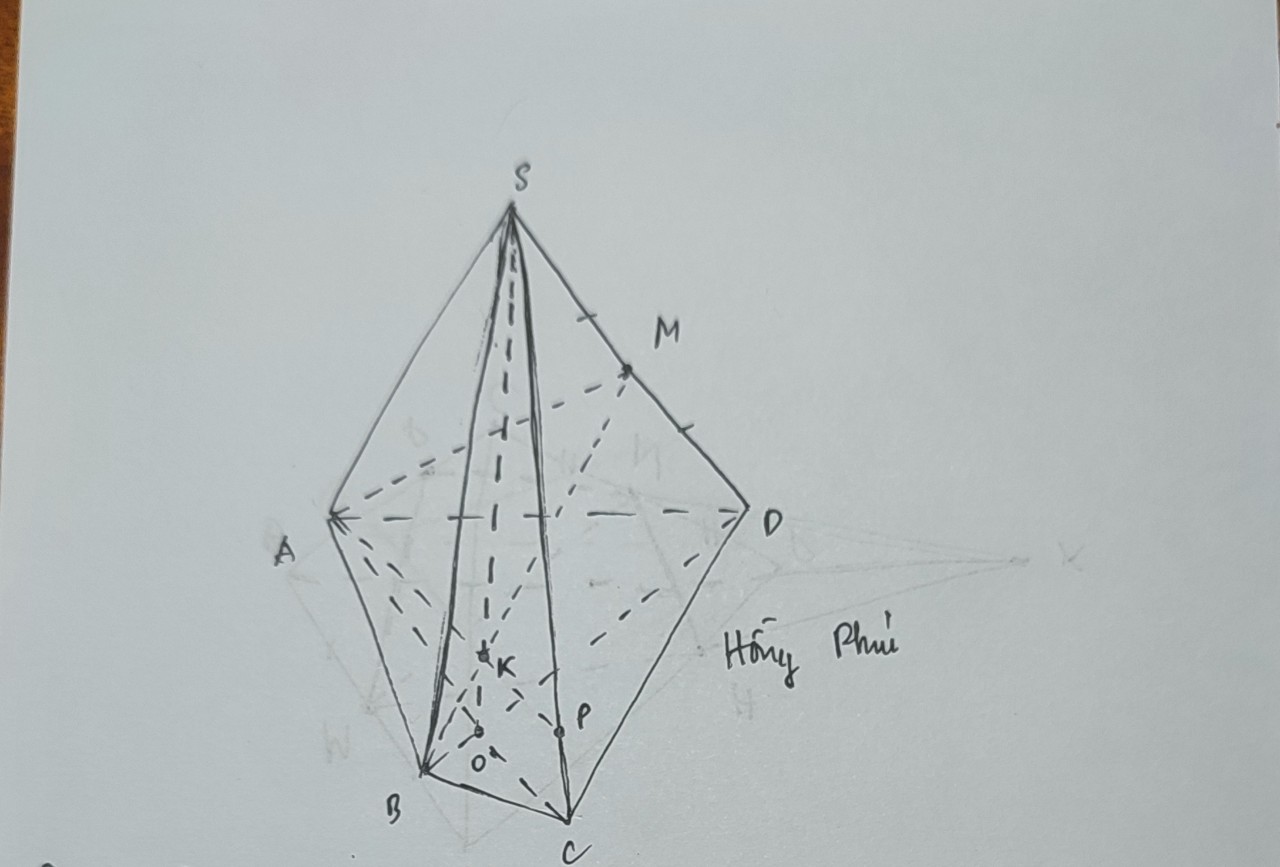
a: Gọi O là giao điểm của AC và BD
\(O\in AC\subset\left(SAC\right)\)
\(O\in BD\subset\left(SBD\right)\)
Do đó: \(O\in\left(SAC\right)\cap\left(SBD\right)\)
mà \(S\in\left(SAC\right)\cap\left(SBD\right)\)
nên \(\left(SAC\right)\cap\left(SBD\right)=SO\)
Gọi K là giao điểm của AB và CD
\(K\in AB\subset\left(SAB\right)\)
\(K\in CD\subset\left(SCD\right)\)
Do đó: \(K\in\left(SAB\right)\cap\left(SCD\right)\)
mà \(S\in\left(SAB\right)\cap\left(SCD\right)\)
nên \(\left(SAB\right)\cap\left(SCD\right)=SK\)
b: Xét (SAD) và (SBC) có
\(S\in\left(SAD\right)\cap\left(SBC\right)\)
AD//BC
Do đó: (SAD) giao (SBC)=xy, xy đi qua S và xy//AD//BC
c: Chọn mp(SCD) có chứa CD
\(N\in SC\subset\left(SCD\right)\)
\(P\in SD\subset\left(SCD\right)\)
Do đó: \(NP\subset\left(SCD\right)\)
mà \(NP\subset\left(MNP\right)\)
nên (SCD) giao (MNP)=NP
Gọi E là giao điểm của CD với NP
=>E là giao điểm của CD với (MNP)
Chọn mp(SBD) có chứa MP
\(BD\subset\left(SBD\right)\)
\(BD\subset\left(ABCD\right)\)
Do đó: \(BD\subset\left(SBD\right)\cap\left(ABCD\right)\)
Gọi F là giao điểm của MP với BD
=>F là giao điểm của MP với (ABCD)

a: \(D\in SD\)
\(D\in\left(ABCD\right)\)
Do đó: \(SD\cap\left(ABCD\right)=D\)
b: Chọn mp(ABCD) có chứa CD
\(AB\subset\left(ABCD\right)\)
\(AB\subset\left(SAB\right)\)
Do đó: \(\left(SAB\right)\cap\left(ABCD\right)=AB\)
Gọi K là giao của AB và CD
=>\(K=CD\cap\left(SAB\right)\)


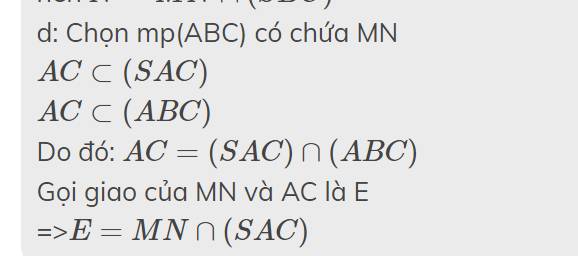
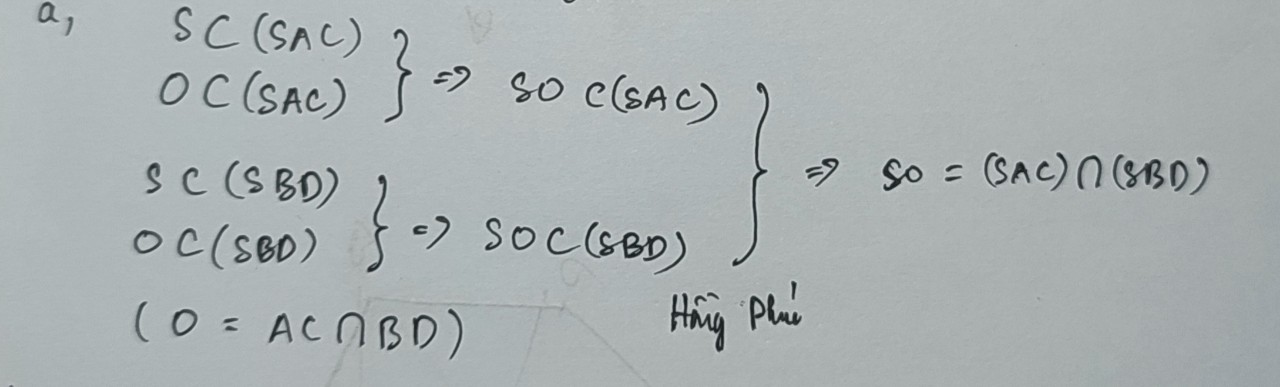
a) Để tìm giao điểm của đường thẳng SB và mặt phẳng (ABC), chúng ta cần tìm điểm giao nhau của đường thẳng SB và mặt phẳng (ABC). Điểm này sẽ nằm trên cả hai đường thẳng SB và mặt phẳng (ABC). Để tìm điểm này, ta có thể sử dụng phương pháp giao điểm giữa đường thẳng và mặt phẳng. Đầu tiên, ta tìm vector pháp tuyến của mặt phẳng (ABC), bằng cách lấy tích vector của hai vector chỉ phương của hai đoạn thẳng AB và AC, ví dụ như vector AB và vector AC. Sau đó, ta tìm phương trình đường thẳng SB, có thể được xác định bằng cách sử dụng hai điểm S và B. Cuối cùng, ta giải hệ phương trình giữa phương trình đường thẳng SB và phương trình mặt phẳng (ABC) để tìm điểm giao nhau.
b) Tương tự, để tìm giao điểm của đường thẳng HB và mặt phẳng (SAC), ta có thể sử dụng phương pháp tương tự như trên. Đầu tiên, ta tìm vector pháp tuyến của mặt phẳng (SAC), bằng cách lấy tích vector của hai vector chỉ phương của hai đoạn thẳng SA và SC, ví dụ như vector SA và vector SC. Sau đó, ta tìm phương trình đường thẳng HB, có thể được xác định bằng cách sử dụng hai điểm H và B. Cuối cùng, ta giải hệ phương trình giữa phương trình đường thẳng HB và phương trình mặt phẳng (SAC) để tìm điểm giao nhau.
c) Để tìm giao điểm của đường thẳng BK và mặt phẳng (SAC), ta cũng có thể sử dụng phương pháp tương tự như trên. Đầu tiên, ta tìm vector pháp tuyến của mặt phẳng (SAC), bằng cách lấy tích vector của hai vector chỉ phương của hai đoạn thẳng SA và SC, ví dụ như vector SA và vector SC. Sau đó, ta tìm phương trình đường thẳng BK, có thể được xác định bằng cách sử dụng hai điểm B và K. Cuối cùng, ta giải hệ phương trình giữa phương trình đường thẳng BK và phương trình mặt phẳng (SAC) để tìm điểm giao nhau.
d) Tương tự, để tìm giao điểm của đường thẳng HK và mặt phẳng (ABC), ta có thể sử dụng phương pháp tương tự như trên. Đầu tiên, ta tìm vector pháp tuyến của mặt phẳng (ABC), bằng cách lấy tích vector của hai vector chỉ phương của hai đoạn thẳng AB và AC, ví dụ như vector AB và vector AC. Sau đó, ta tìm phương trình đường thẳng HK, có thể được xác định bằng cách sử dụng hai điểm H và K. Cuối cùng, ta giải hệ phương trình giữa phương trình đường thẳng HK và phương trình mặt phẳng (ABC) để tìm điểm giao nhau.