Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi K là trung điểm của CD
Xét ΔADC có
Q,K lần lượt là trung điểm của DA,DC
=>QK là đường trung bình của ΔADC
=>QK//AC
=>Hình chiếu song song của điểm Q theo phương AC lên mp(BCD) là điểm K

Gọi N là trung điểm của SD
Xét ΔSCD có
M,N lần lượt là trung điểm của SC,SD
=>MN là đường trung bình của ΔSCD
=>MN//CD
=>MN//AB
=>N là hình chiếu song song của M theo phương AB lên mp(SAD)

Vì M, N, P lần lượt là trung điểm của AB, AC, AD nên MN, NP, MP lần lượt là đường trung bình của tam giác ABC, ACD, ABD
⇒ MN//BC, NP//CD, PM //BD
Mà BC, CD, BD thuộc (BCD)
MN, NP, PM không thuộc (BCD)
⇒ Các đường thẳng MN, NP, PM có song song với mặt phẳng (BCD)

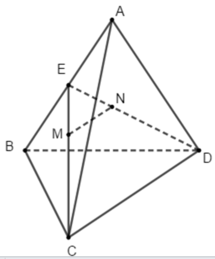
Gọi E là trung điểm của AB.M, N lần lượt là trọng tâm của tam giác ABC, ABD nên:
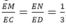
Theo định lí Ta-lét ta có MN // CD. Vậy hình chiếu song song của điểm M theo phương CD lên mặt phẳng (ABD) là trọng tâm của tam giác ABD. Đáp án C.

Gọi M là trung điểm của SA
Xét ΔSAD có
M,N lần lượt là trung điểm của SA,SD
=>MN là đường trung bình của ΔSAD
=>MN//AD
=>MN//BC
=>M là hình chiếu song song của N theo phương BC lên mp(SAB)

△ABC có: M, N là trung điểm của AB, AC
Suy ra: MN // BC nên MN // (BCD).
△ACD có: N, P là trung điểm của AC, AD
Suy ra: NP // CD nên NP // (BCD).
△ABD có: M, P là trung điểm của AB, AD
Suy ra: MP // BD nên MP // (BCD).
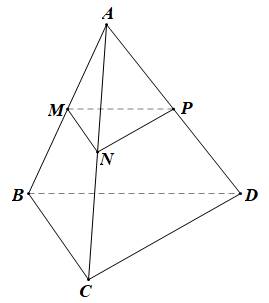
• Xét DABC có M, N lần lượt là trung điểm của AB, AC nên MN là đường trung bình của tam giác
Do đó MN // BC
Lại có BC ⊂ (BCD)
Suy ra MN // (BCD).
• Chứng minh tương tự ta cũng có NP // CD.
Mà CD ⊂ (BCD)
Suy ra NP // (BCD).
• Tương tự, MP // BD mà BD ⊂ (BCD) .
Suy ra MP // (BCD).
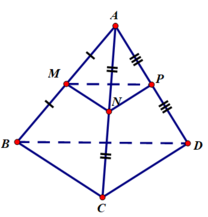
Gọi N là trung điểm của BC
Xét ΔABC có
N,P lần lượt là trung điểm của BC,BA
=>NP là đường trung bình của ΔABC
=>NP//AC
=>Hình chiếu song song của điểm P theo phương AC lên mp(BCD) là điểm N