Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

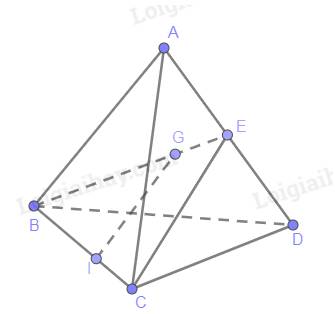
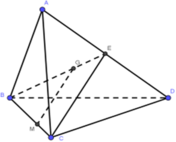
Tam giác BCE có E là trung điểm AD
Suy ra:\(\frac{{BG}}{{BE}} = \frac{{BI}}{{BC}} = \frac{2}{3}\)
Theo Ta lét, IG //CE
Mà CE thuộc (ACD)
Suy ra: IG // (ACD)

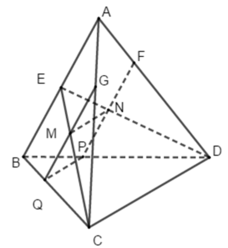
(∝) // AB nên giao tuyến của (∝) với (ABC) là đường thẳng qua M, song song với AB, cắt BC tại Q, cắt AC tại G
(∝) // AB nên giao tuyến của (∝) với (ABC) là đường thẳng qua N, song song với AB, cắt BD tại P, cắt AD tại F
Gọi E là trung điểm của AB. M, N lần lượt là trọng tâm các tam giác ABC, ABD nên
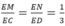
theo định lí Ta- lét ta có MN // CD.
Do MN // CD nên PQ // GF // CD, lại có QG // FP(//AB nên thiết diện là hình bình hành GQPF.
Đáp án B

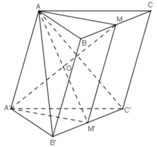
a) Do ABC.A’B’C’ là hình lăng trụ nên ta có: BCC’B’ là hình bình hành
Xét tứ giác BCC’B’ có M và M’ lần lượt là trung điểm của BC và B’C’ nên MM’ là đường trung bình
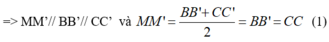
Lại có: AA’// BB’ và AA’= BB’ ( tính chất hình lăng trụ) (2)
Từ (1) và (2) suy ra: MM’// AA’ và MM’ = AA’
=> Tứ giác AMM’A’ là hình bình hành
b) Trong (AMM’A’) gọi O = A’M ∩ AM’, ta có :
Ta có : O ∈ AM’ ⊂ (AB’C’)
⇒ O = A’M ∩ (AB’C’).
c)
Gọi K = AB’ ∩ BA’, ta có :
K ∈ AB’ ⊂ (AB’C’)
K ∈ BA’ ⊂ (BA’C’)
⇒ K ∈ (AB’C’) ∩ (BA’C’)
Dễ dàng nhận thấy C’ ∈ (AB’C’) ∩ (BA’C’)
⇒ (AB’C’) ∩ (BA’C’) = KC’.
Vậy d cần tìm là đường thẳng KC’
d) Trong mp(AB’C’), gọi C’K ∩ AM’ = G.
Ta có: G ∈ AM’ ⊂ (AM’M)
G ∈ C’K.
⇒ G = (AM’M) ∩ C’K.
+ K = AB’ ∩ A’B là hai đường chéo của hình bình hành ABB’A’
⇒ K là trung điểm AB’.
ΔAB’C’ có G là giao điểm của 2 trung tuyến AM’ và C’K
⇒ G là trọng tâm ΔAB’C’.

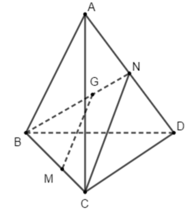
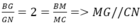
Gọi E là trung điểm của AB.M, N lần lượt là trọng tâm của tam giác ABC, ABD nên:
Theo định lí Ta-lét ta có MN // CD. Vậy hình chiếu song song của điểm M theo phương CD lên mặt phẳng (ABD) là trọng tâm của tam giác ABD. Đáp án C.