Cho tứ diện ABCD. Gọi M, N là trung điểm của AD, BC. Khẳng định nào sau đây đúng?

K

Khách

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn lớp

Chọn môn

Mua vip

PT

Pham Trong Bach

6 tháng 2 2018

Cho tứ diện ABCD. Gọi M, N là trung điểm của AD, BC. Khẳng định nào sau đây đúng?

#Toán lớp 11

1

CM

Cao Minh Tâm

6 tháng 2 2018

Các câu hỏi dưới đây có thể giống với câu hỏi trên

PT

Pham Trong Bach

26 tháng 6 2019

Cho tứ diện ABCD, G là trọng tâm tam giác ABD, N là trung điểm của AD, M là trung điểm trên cạnh BC sao cho MB = 2MC. Khẳng định nào sau đây là đúng?

A. MG // CN

B. MG và CN cắt nhau

C. MG // AB

D. MG và CN chéo nhau.

#Toán lớp 11

1

CM

Cao Minh Tâm

26 tháng 6 2019

G là trọng tâm của tam giác ABD nên

Bài tập trắc nghiệm Hình học 11 | Câu hỏi trắc nghiệm Hình học 11

Đáp án A

PT

Pham Trong Bach

20 tháng 6 2018

Cho tứ diện ABCD có AC = AD và BC = BD. Gọi I là trung điểm của CD. Khẳng định nào sau đây sai?

A. Góc giữa hai mặt phẳng (ABC) và (ABD) là C B D ^

B. Góc giữa hai mặt phẳng (ACD) và (BCD) là A I B ^

C. (BCD) ⊥ (AIB).

D. (ACD) ⊥ (AIB).

#Toán lớp 11

1

CM

Cao Minh Tâm

20 tháng 6 2018

Chọn A.

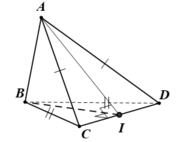
Đề kiểm tra 45 phút Hình học 11 Chương 3 có đáp án (Đề 1)

+) Tam giác BCD có BC = BD nên cân tại B: Có BI là đường trung tuyến nên đồng thời là đường cao: CD ⊥ BI (1)

+) Tam giác ACD có AC = AD nên cân tại A: Có AI là đường trung tuyến nên đồng thời là đường cao: CD ⊥ AI (2)

- Từ (1) và (2) ⇒ CD ⊥ (ABI) (3)

+) Vì:

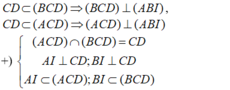
Đề kiểm tra 45 phút Hình học 11 Chương 3 có đáp án (Đề 1)

- Suy ra: góc giữa hai mặt phẳng (ACD) và (BCD) là 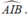Đề kiểm tra 45 phút Hình học 11 Chương 3 có đáp án (Đề 1)

- Vậy: A sai.

PT

Pham Trong Bach

7 tháng 1 2019

Cho tứ diện ABCD. Gọi M và P lần lượt là trung điểm của AB và CD. Đặt A B → = b → ; A C → = c → ; A D → = d . Khẳng định nào sau đây đúng? ...

#Toán lớp 11

1

CM

Cao Minh Tâm

7 tháng 1 2019

ĐÁP ÁN: A

PT

Pham Trong Bach

18 tháng 2 2018

Cho tứ giác ABCD. Gọi M, N, P, Q lần lượt là trung điểm AB, BC, CD, DA. Khẳng định nào sau đây đúng A. B. C. ...

#Toán lớp 11

1

CM

Cao Minh Tâm

18 tháng 2 2018

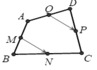
+Do M, N lần lượt là trung điểm của AB và BC nên MN là đường trung bình của tam giác ABC

NT

NgUyễn THi tHục

15 tháng 12 2023

cho tứ diện ABCD gọi E là trung điểm DC, M là điểm nằm giữa A và E hình chiếu song song của M lên (BCD) theo phương chiếu AD là M' khẳng định nào sau đây đúng?
A. M' thuộc đoạn BE

B. M' thuộc đoạn BC

C. M' thuộc đoạn BD

D. M' thuộc đoạn CD

#Toán lớp 11

1

PV

Phan Văn Toàn

15 tháng 12 2023

A

PT

Pham Trong Bach

15 tháng 1 2017

Cho tứ diện ABCD, biết hai tam giác ABC và BCD là hai tam giác cân có chung cạnh đáy BC. Gọi I là trung điểm của cạnh BC. Khẳng định nào đúng trong các khẳng định sau? A. B C ⊥ A D I B. A B ⊥ A D I C. A I ⊥ B C D D. A C ⊥ A D I ...

#Toán lớp 11

1

CM

Cao Minh Tâm

15 tháng 1 2017

Chọn A.

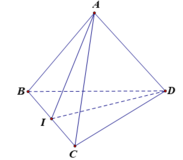
Đề thi Học kì 2 Toán 11 có đáp án (Đề 1)

+) Tam giác ABC cân tại A có AI là đường trung tuyến nên đồng thời là đường cao: AI ⊥ BC (1)

+) Tam giác BCD cân tại D có DI là đường trung tuyến nên đồng thời là đường cao: DI ⊥ BC (2)

- Từ (1) và (2) suy ra BC ⊥ (ADI).

PT

Pham Trong Bach

24 tháng 9 2018

Cho tứ diện ABCD, G là trọng tâm của tam giác ABD, M là điểm trên cạnh BC sao cho MB = 2MC. Khẳng định nào sau đây là đúng?

A. MG // (ACD)

B. MG // (ABC)

C. MG // AB

D. MG cắt AC

#Toán lớp 11

1

CM

Cao Minh Tâm

24 tháng 9 2018

Gọi N là trung điểm của AD

G là trọng tâm của tam giác ABD nên:

Bài tập trắc nghiệm Hình học 11 | Câu hỏi trắc nghiệm Hình học 11

⇒ MG // CN.

Do CN thuộc (ACD) nên MG // (ACD).

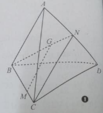
Bài tập trắc nghiệm Hình học 11 | Câu hỏi trắc nghiệm Hình học 11

Đáp án A

PT

Pham Trong Bach

1 tháng 8 2017

Cho tứ diện ABCD. Gọi M, N, P, Q lần lượt là trung điểm của các cạnh AB, AD, CD, BC. Mệnh đề nào sau đây sai ?

A. MN// BD và M N = 1 2 B D

B. MN // PQ và MN = PQ.

C. MNPQ là hình bình hành.

D. MP và NQ chéo nhau.

#Toán lớp 11

1

CM

Cao Minh Tâm

1 tháng 8 2017

Chọn D.

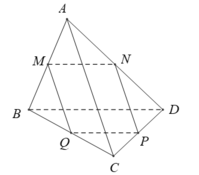
Đề kiểm tra 45 phút Hình học 11 Chương 2 có đáp án (Đề 1)

- Vì MN, PQ lần lượt là đường trung bình tam giác ABD, BCD nên:

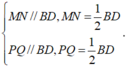
Đề kiểm tra 45 phút Hình học 11 Chương 2 có đáp án (Đề 1)

- Nên MN // PQ, MN = PQ.

⇒ tứ giác MNPQ là hình bình hành.

- Do đó MP và NQ cùng thuộc mặt phẳng MNPQ và hai đường thẳng này cắt nhau.

PT

Pham Trong Bach

26 tháng 5 2018

Cho tứ diện ABCD, các điểm E, F, G, H lần lượt thuộc các cạnh AD, AB, BC, CD sao cho E A E D = F A F B = G C G B = H C H D Khẳng định nào sau đây là đúng? A. EFGH là hình bình hành. B. EFGH có đúng một cặp cạnh song song. C. EFGH là tứ giác không có cặt cạnh nào song song. D. EFGH là hình chữ...

#Toán lớp 11

1

CM

Cao Minh Tâm

26 tháng 5 2018

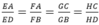
Bài tập trắc nghiệm Hình học 11 | Câu hỏi trắc nghiệm Hình học 11

⇒ FG // EH // AC, EF // GH // BD

Vậy EFGH là hình bình hành

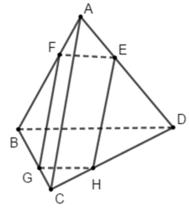
Đáp án A