Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B.
*Xác định tâm mặt cầu ngoại tiếp hình chóp A.BCHK
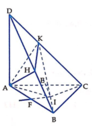
Gọi E, F lần lượt là trung điểm của AC và AB. Trong mặt phẳng (ABC), kẻ các đường thẳng d, d’ lần lượt vuông góc với AC và AB tại E, F. Do D A ⊥ d , D A ⊥ d ' (do D A ⊥ A B C ) nên d ⊥ D A C , d ' ⊥ D A B . Gọi I là giao điểm của d, d’ thì I chính là tâm của mặt cầu chứa hai đường tròn ngoại tiếp hai tam giác AHC, AKC. Hay nói cách khác, I là tâm mặt cầu ngoại tiếp hình chóp A.BCHK, bán kính R = IA cũng chính là bán kính đường tròn ngoại tiếp Δ A B C (do IA = IB = IC).
*Một số hệ thức cần nhớ trong tam giác
Cho Δ A B C , gọi AH là đường cao H ∈ B C . R, r lần lượt là bán kính đường tròn ngoại tiếp và đường tròn nội tiếp tam giac, p là nửa chu vi. Kí hiệu BC = a, AC = b, AB = c, diện tích S Δ A B C = S .
1. Định lý cosin:
a 2 = b 2 + c 2 − 2 b c cos A ; b 2 = a 2 + c 2 − 2 a c cos B ; c 2 = a 2 + b 2 − 2 a b cos C .
2. Định lý sin: a sin A = b sin B = c sin C = 2 R .
3. Độ dài trung tuyến xuất phát từ các đỉnh A, B, C (Kí hiệu lần lượt là m a , m b , m c ):
m a 2 = b 2 + c 2 2 − a 2 4 ; m b 2 = a 2 + c 2 2 − b 2 4 ; m c 2 = a 2 + b 2 2 − c 2 4 .4. Các công thức tính diện tích tam giác:
S = 1 2 a . h a = 1 2 b . h b = 1 2 c . h c S = 1 2 b c sin A = 1 2 a c sin B = 1 2 a b sin C S = a b c 4 R = p r = p p − a p − b p − c .5. Định lý tang:
a − b a + b = tan A − B 2 tan A + B 2 ; b − c b + c = tan B − C 2 tan B + C 2 ; c − a c + a = tan C − A 2 tan C + A 2 .
6. Định lý cotang:
cot A = b 2 + c 2 − a 2 4 S ; cot B = a 2 + c 2 − b 2 4 S ; cot C = a 2 + b 2 − c 2 4 S . → cot A + cot B + cot C = a 2 + b 2 + c 2 4 S .
*Phân tích dữ kiện đề bài:
cot A + cot B + cot C 2 = B C A B . A C + C A B A . B C + A B C A . C B ⇔ A B 2 + B C 2 + C A 2 8 S Δ A B C = B C 2 + C A 2 + A B 2 A B . A C . B C ⇔ 8 S Δ A B C = A B . A C . B C ⇔ 8. A B . A C . B C 4 R = A B . A C . B C ⇔ R = 2 = I A .
Vậy thể tích mặt cầu ngoại tiếp hình chóp A.BCHK là:
V = 4 3 π R 3 = 4 3 π 2 3 = 32 π 3 (đvtt).

Đáp án B
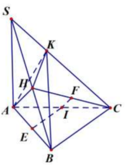
Gọi I, E, F lần lượt là trung điểm của AC, AB, HC. IE là trục đường tròn ngoại tiếp tam giác AHB, IF là trục đường tròn ngoại tiếp tam giác HKC.
=> IA = IB = IC = IH = IK
Suy ra I là tâm mặt cầu ngoại tiếp tứ diện AHKB.
Suy ra bán kính R = 2 π a 3 3

Đáp án B
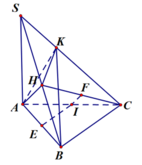
Gọi I, E, F lần lượt là trung điểm của AC, AB, HC.
IE là trục đường tròn ngoại tiếp tam giác AHB, IF là trục đường tròn ngoại tiếp tam giác HKC.
Suy ra I là tâm mặt cầu ngoại tiếp tứ diện AHKB. Suy ra bán kính R = a 2 2

Theo giả thiết, ta có ![]() và
và ![]()
Do 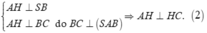
Từ (1) và (2) suy ra ba điểm B, H, K cùng nhìn xuống AC dưới một góc 90 ° nên
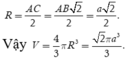
Chọn C.

Chọn A.
Phương pháp:
Xác định tâm, bán kính của khối cầu.
Thể tích khối cầu có bán kính r là:
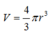
Cách giải:
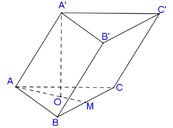
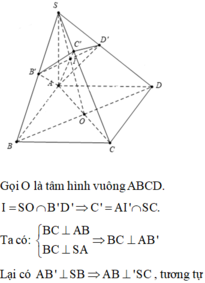
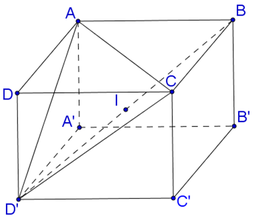
Gọi O là tâm đường tròn ngoại tiếp
DABC, đường kính AD.
Ta chứng minh O là tâm mặt cầu đi qua 6 điểm A, B, C, B 1 , C 1 và D
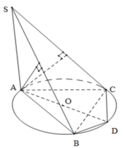

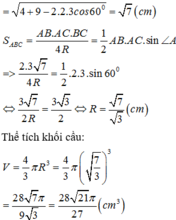




Đáp án A
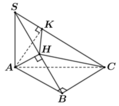
Gọi I là tâm đường tròn ngoại tiếp tam giác ABC. Do tam giác AHB vuông tại H nên I thuộc trục của tam giác AHB. Tương tự I cũng thuộc trục của tam giác AKC. Suy ra I cách đều A, B, H,K, C nên nó là tâm mặt cầu ngoại tiếp hình chóp A.BCKH.
Gọi R là bán kính mặt cầu ngoại tiếp hình chóp A.BCKH thì R cũng là bán kính đường tròn ngoại tiếp tam giác ABC.
Ta có:
cot A + cot B + cot C = b 2 + c 2 - a 2 4 S + a 2 + c 2 - b 2 4 S + a 2 + b 2 - c 2 4 S = a 2 + b 2 + c 2 4 S
Nên c o t A + c o t B + c o t C 2 = B C A B . A C + C A B C . B A + A B C A . C B
⇔ a 2 + b 2 + c 2 8 S = a . sin A b c . sin A + b . sin B c a . sin B + c . sin C a b . sin C
⇔ a 2 + b 2 + c 2 8 S = a 2 4 R S + b 2 4 R S + c 2 4 R S ⇔ R = 2 ⇒ V = 4 3 πR 3 = 32 π 3