Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Vì B A C ^ = 90 o nên BC = 5. Khi đó
S 1 S 2 = π . 4 . 5 π . 3 . 5 = 4 3
Đáp án A

Chọn C.
Phương pháp:
Dựng hình, xác định các hình tròn xoay tạo thành khi quay và tính tỉ số thể tích.
Cách giải:
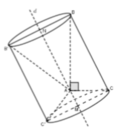
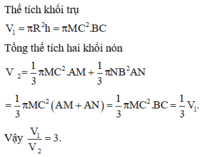

Đáp án B
Gọi H là hình chiếu của C trên AB. Khi quay quanh AB ta sẽ thu được một hình nón bị thiếu đáy và thể tích phần đáy bị thiếu lại chính bằng thể tích của khối nón nhỏ khi quay ∆ A B C quanh AH. Vậy thể tích cần tính là
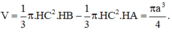

Đáp án C
Khi quay tam giác theo BC ta sẽ có được hai khối nón như hình vẽ.
Trong ΔABC, gọi H là chân đường cao của A đến BC. Ta có


Đáp án C
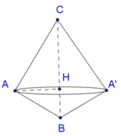
Khi quay tam giác theo BC ta sẽ có được hai khối nón như hình vẽ.
Trong ∆ A B C , gọi là H chân đường cao của A đến BC. Ta có


Đáp án B
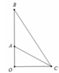
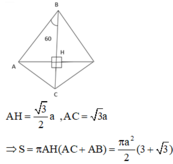
Ta có V = 1 3 π . OC 2 . BO - 1 3 πOC 2 . AO = 1 3 π . OC 2 . AB .
Lại có sin 60 ° = O C A C ⇒ O C = a 3 2 ⇒ V = πa 3 4 .
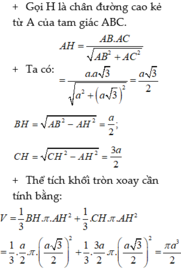

Đáp án A
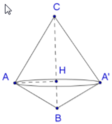
Vì hai mặt phẳng (ABC), (ABD) vuông góc với nhau nên bài toán trở thành “Tính thể tích khối tròn xoay khi quay tam giác HAB quanh AB với ABCD là hình thang vuông tại A,B” như hình bên. Hai tam giác BHC và DHA đồng dạng ⇒ B H D H = H C H A = B C A D = 1 3 .
Mà B D = A D 2 + A B 2 = 2 a 3 ; A C = A B 2 + C B 2 = 2 a
Suy ra A H = 3 4 A C = 3 4 .2 a = 3 a 2 và B H = 1 4 B D = 1 4 .2 a 3 = a 3 2 .
Diện tích tam giác ABH là:
S Δ A B H = 1 2 . A H . B H = 1 2 . 3 a 2 . a 3 2 = 3 a 2 3 8 = 1 2 . d H ; B C . B C ⇒ d H ; B C = 2. 3 a 2 3 8 . a 3 = 3 a 4 .
Vậy thể tích khối tròn xoay cần tính là:
V = 1 3 π 3 a 4 2 . a 3 = 3 3 π a 2 16 .