Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có hình vẽ:
Vì \(Pm\) là tia phân giác của góc \(\widehat{xOy}\) nên
\(\widehat{POx}=\widehat{mOx}=\dfrac{1}{2}\widehat{xOy}\)
Vì \(Pa\) và \(Pb\) nằm ở 2 nửa mặt phẳng khác nhau nên:
\(aP\) đối \(Py\) và \(bP\) đối \(Px\)
Vì \(\widehat{aPm}=\widehat{bPm}=\dfrac{1}{2}\widehat{xPy}\)
Nên:
\(\widehat{aPm}+\widehat{bPm}=\widehat{xPy}=\widehat{aPb}\)
Vậy 2 góc trên đối đỉnh

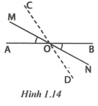
Theo đề bài ta có A O M ^ = M O C ^ , B O N ^ = D O N ^ mà A O M ^ = B O N ^ (hai góc đối đỉnh) nên M O C ^ = D O N ^ .
Ta có M O D ^ + D O N ^ = 180 ° (hai góc kề bù), suy ra M O D ^ + M O C ^ = 180 ° .
Hai góc MOD và MOC là hai góc kề, có tổng bằng 180 ° nên hai tia OC, OD đối nhau.
Chứng tỏ một tia là tia phân giác
Mình làm đk rùi lên mình k cần các bạn giải nx nhé...>_^