Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1/
a/ \(\frac{x}{-3,7}=\frac{-2,5}{0,25}\)
=> \(0,25x=\left(-2,5\right)\left(-3,7\right)\)
=> \(0,25x=9,25\)
=> \(x=\frac{9,25}{0,25}\)
=> \(x=37\)
b/ Bạn coi lại đề.
2/
a/ \(\frac{a}{b}=\frac{c}{d}\)<=> \(\frac{a+b}{b}=\frac{c+d}{d}\)
Ta có \(\frac{a}{b}=\frac{c}{d}\)
=> \(\frac{a}{c}=\frac{b}{d}=\frac{a+b}{c+d}\)(tính chất tỉ lệ thức)
=> \(\frac{a}{c}=\frac{b}{d}=\frac{a+b}{c+d}\)(tính chất dãy tỉ số bằng nhau)
Ta lại có \(\frac{a+b}{c+d}=\frac{b}{d}\)
=> \(\frac{a+b}{b}=\frac{c+d}{d}\)(tính chất tỉ lệ thức) (đpcm)

Đặt \(\frac{a}{b}=\frac{c}{d}=k\Rightarrow a=bk;c=dk\)
\(\left(\frac{a+b}{c+d}\right)^3=\left(\frac{bk+b}{dk+d}\right)^3=\left(\frac{b\left(k+1\right)}{d\left(k+1\right)}\right)^3=\left(\frac{b}{d}\right)^3\left(1\right)\)
\(\frac{a^3+b^3}{c^3+d^3}=\frac{\left(bk\right)^3+b^3}{\left(dk\right)^3+d^3}=\frac{b^3k^3+b^3}{d^3k^3+d^3}=\frac{b^3\left(k^3+1\right)}{d^3\left(k^3+1\right)}=\frac{b^3}{d^3}=\left(\frac{b}{d}\right)^3\left(2\right)\)
Từ (1) & (2)=>\(\left(\frac{a+b}{c+d}\right)^3=\frac{a^3+b^3}{c^3+d^3}\)

a/b=c/d=k
=>a=bk; c=dk
\(\dfrac{3b+5d}{3a+5c}=\dfrac{3b+5d}{3bk+3dk}=\dfrac{1}{k}\)
\(\dfrac{b-2d}{a-2c}=\dfrac{b-2d}{bk-2dk}=\dfrac{1}{k}\)
=>\(\dfrac{3b+5d}{3a+5c}=\dfrac{b-2d}{a-2c}\)
b: \(\dfrac{ab}{a^2-b^2}=\dfrac{bk\cdot b}{b^2k^2-b^2}=\dfrac{k}{k^2-1}\)
\(\dfrac{cd}{c^2-d^2}=\dfrac{dk\cdot d}{d^2k^2-d^2}=\dfrac{k}{k^2-1}\)
=>ab/a^2-b^2=cd/c^2-d^2
c: \(\dfrac{a^2+b^2}{\left(a+b\right)^2}=\dfrac{b^2k^2+b^2}{\left(bk+b\right)^2}=\dfrac{k^2+1}{\left(k+1\right)^2}\)
\(\dfrac{c^2+d^2}{\left(c+d\right)^2}=\dfrac{d^2k^2+d^2}{\left(dk+d\right)^2}=\dfrac{k^2+1}{\left(k+1\right)^2}\)
=>\(\dfrac{a^2+b^2}{\left(a+b\right)^2}=\dfrac{c^2+d^2}{\left(c+d\right)^2}\)

Câu 1
Ta có : \(\frac{a}{b}=\frac{c}{d}=>\left(\frac{a}{b}+1\right)=\left(\frac{c}{d}+1\right)\left(=\right)\frac{a+b}{b}=\frac{c+d}{d}\)
=> ĐPCM
Câu 2
Ta có \(\frac{a}{b}=\frac{c}{d}=>\frac{b}{a}=\frac{d}{c}=>\left(\frac{b}{a}+1\right)=\left(\frac{d}{c}+1\right)\left(=\right)\frac{b+a}{a}=\frac{d+c}{c}=>\frac{a}{b+a}=\frac{c}{d+c}\)
=> ĐPCM
Câu 3
Câu 3
Ta có \(\frac{a+b}{a-b}=\frac{c+d}{c-d}\)(=) (a+b).(c-d)=(a-b).(c+d)(=)ac-ad+bc-bd=ac+ad-bc-bd(=)-ad+bc=ad-bc(=) bc+bc=ad+ad(=)2bc=2ad(=)bc=ad=> \(\frac{a}{b}=\frac{c}{d}\)
=> ĐPCM
Câu 4
Đặt \(\frac{a}{b}=\frac{c}{d}=k\)
\(=>\hept{\begin{cases}a=bk\\c=dk\end{cases}}\)
Ta có \(\frac{ac}{bd}=\frac{bk.dk}{bd}=k^2\left(1\right)\)
Lại có \(\frac{a^2+c^2}{b^2+d^2}=\frac{b^2k^2+c^2k^2}{b^2+d^2}=\frac{k^2.\left(b^2+d^2\right)}{b^2+d^2}=k^2\left(2\right)\)
Từ (1) và (2) => ĐPCM
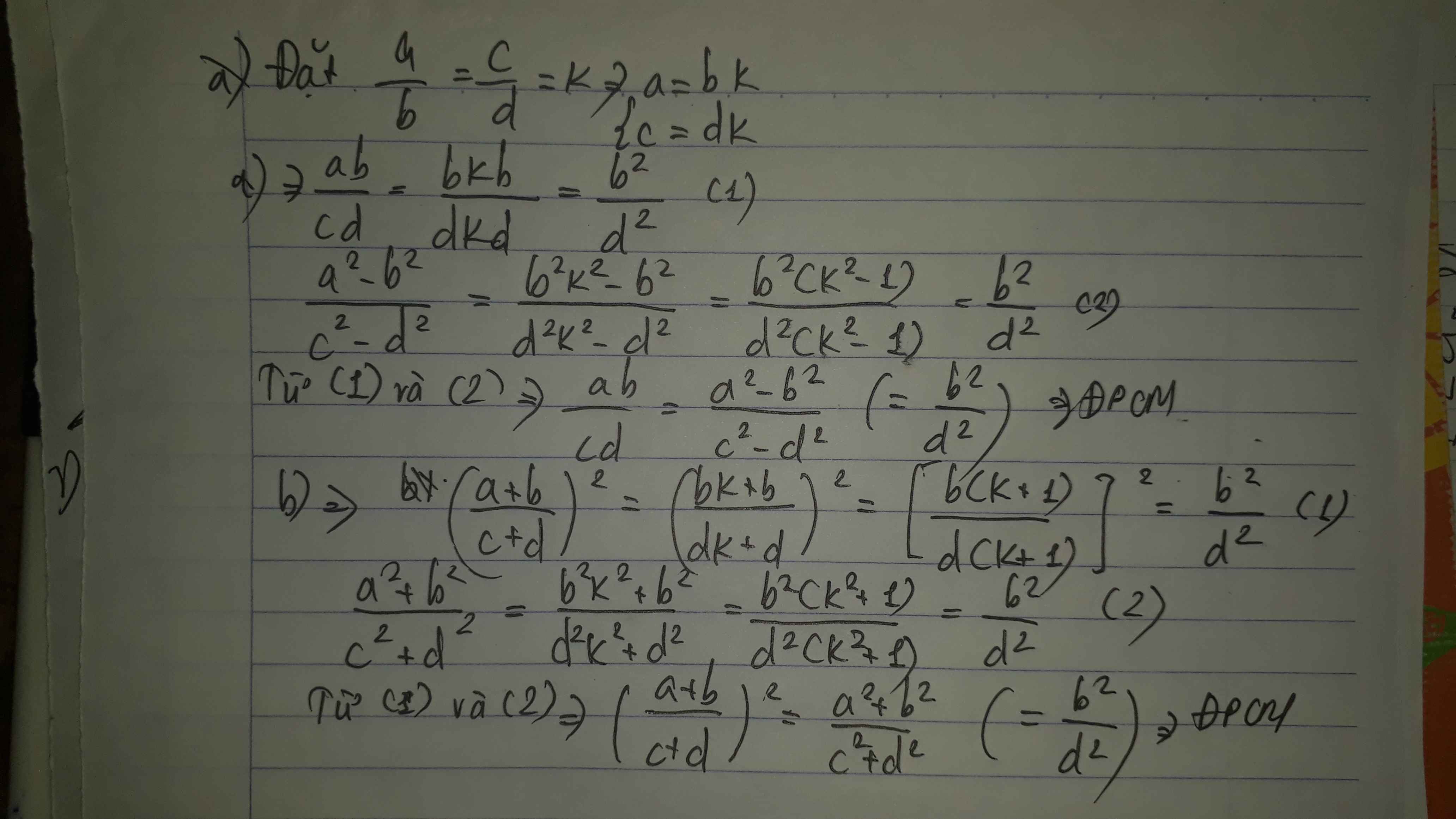
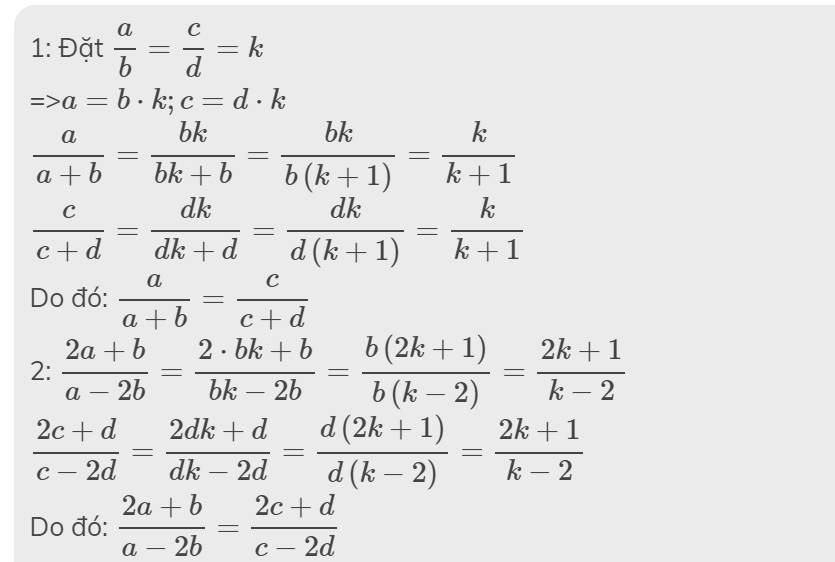
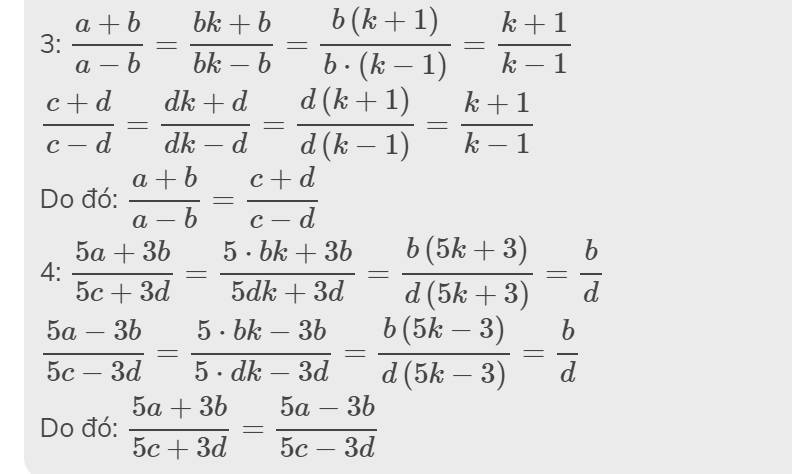
Đặt \(\frac{a}{b}=\frac{c}{d}=k\Rightarrow a=bk;c=dk\)
\(\frac{a^2-b^2}{ab}=\frac{\left(bk\right)^2-b^2}{bk.b}=\frac{b^2.k^2-b^2}{b^2k}=\frac{b^2\left(k^2-1\right)}{b^2k}=\frac{k^2-1}{k}\left(1\right)\)
\(\frac{c^2-d^2}{cd}=\frac{\left(dk\right)^2-d^2}{dk.d}=\frac{d^2k^2-d^2}{d^2k}=\frac{d^2\left(k^2-1\right)}{d^2.k}=\frac{k^2-1}{k}\left(2\right)\)
Từ (1) và (2)=>\(\frac{a^2-b^2}{ab}=\frac{c^2-d^2}{cd}\).
phần b đề kiểu gì vậy??//