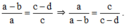Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

ta có:a/b=c/d
=>a/c=b/d
áp dụng tích chất dãy tỉ số bằng nhau ta có:
a/c=b/d=a+b/c+d=a-c/c-d
=>a+b/c+d=a-b/c-d
do đó: a+b/a-c=c+d/c-d
ta có;
a/b=c/d =>a/c=b/d
áp dụng tích chất dãy tỉ số bằng nhau ta có:
a/c=b/d =>a+b/c+d=a-b/c-d
=>a+b/c+d=a-b/c-d => a+b/a-b=c+d/c-d

Ta có : a+b/b+c = c+d/d+a
=> (a+b)/(c+d)= (b+c)/(d+a)
=> (a+b)/(c+d)+1=(b+c)/(d+a)+1
hay: (a+b+c+d)/(c+d)=(b+c+d+a)/(d+a)
- Nếu a+b+c+d khác 0 thì : c+d=d+a => c=a (1)
- Nếu a+b+c+d = 0 (2)
Từ (1) và (2)
\(\RightarrowĐPCM\)
Ta có : \(\frac{a+b}{b+c}=\frac{c+d}{d+a}\)
\(\Rightarrow\)\(\frac{a+b}{c+d}=\frac{b+c}{d+a}\)
\(\Rightarrow\)\(\frac{a+b}{c+d}+1=\frac{b+c}{d+a}+1\)
Hoặc \(\frac{a+b+c+d}{c+d}=\frac{b+c+d+a}{d+a}\)
Nếu a + b + c + d khác 0 thì c + d = d + a => c = a ( hoặc a = c )
Nếu a + b + c + d = 0 ( đpcm )
Chứng minh từ tỉ lệ thức a/b=c/d(a-b khác 0, c-d khác 0) ta có thể suy ra tỉ lệ thức a+b/a-b=c+d/c-d

Đặt \(\dfrac{a}{b}=\dfrac{c}{d}=k\)
\(\Rightarrow a=b.k;b=d.k\)
Ta có:
\(\dfrac{a+b}{a-b}=\dfrac{c+d}{c-d}\Rightarrow\dfrac{a+b}{c+d}=\dfrac{a-b}{c-d}\)
\(+)\dfrac{a+b}{c+d}=\dfrac{b.k+b}{d.k+d}=\dfrac{b.\left(k+1\right)}{d.\left(k+1\right)}=\dfrac{b}{d}\left(1\right)\)
\(+)\dfrac{a-b}{c-d}=\dfrac{b.k-b}{d.k-d}=\dfrac{b.\left(k-1\right)}{d.\left(k-1\right)}=\dfrac{b}{d}\left(2\right)\)
Từ \(\left(1\right)\) và \(\left(2\right)\) \(\Rightarrow\dfrac{a+b}{c+d}=\dfrac{a+b}{c-d}=\dfrac{c+d}{c-d}\left(đpcm\right)\)
Chúc bạn học tốt!

\(\frac{a}{b}< \frac{c}{d}\Rightarrow ad< bc\)
Có:
- \(\frac{ab+ad}{b\left(b+d\right)}< \frac{ab+bc}{b\left(b+d\right)}\)
\(\Rightarrow\frac{a\left(b+d\right)}{b\left(b+d\right)}< \frac{b\left(a+c\right)}{b\left(b+d\right)}\)
\(\Rightarrow\frac{a}{b}< \frac{a+c}{b+d}\left(1\right)\)
- \(\frac{ad+cd}{d\left(b+d\right)}< \frac{bc+cd}{d\left(b+d\right)}\)
\(\Rightarrow\frac{d\left(a+c\right)}{d\left(b+d\right)}< \frac{c\left(b+d\right)}{d\left(b+d\right)}\)
\(\Rightarrow\frac{a+c}{b+d}< \frac{c}{d}\left(2\right)\)
\(\left(1\right)\left(2\right)\Rightarrow\frac{a}{b}< \frac{a+c}{b+d}< \frac{c}{d}\)

\(\frac{a}{b}=\frac{c}{d}\Rightarrow\frac{a}{c}=\frac{b}{d}=\frac{a+b}{c+d}=\frac{a-b}{c-d}\Rightarrow\frac{a+b}{c+d}=\frac{a-b}{c-d}\Rightarrow\frac{a+b}{a-b}=\frac{c+d}{c-d}\)(đpcm)

\(\frac{a}{b}=\frac{c}{d}\Rightarrow ad=bc\Rightarrow\frac{a}{c}=\frac{b}{d}\)
Áp dụng tính chất của dãy tỉ số bằng nhau ta có:
\(\frac{a}{c}=\frac{b}{d}=\frac{a+b}{c+d}=\frac{a-b}{c-d}\)
\(\Rightarrow\left(a+b\right)\left(c-d\right)=\left(a-b\right)\left(c+d\right)\)
\(\Rightarrow\frac{a+b}{a-b}=\frac{c+d}{c-d}\)(điều phải chứng minh)
\(\frac{a}{b}=\frac{c}{d}\Rightarrow\frac{a}{c}=\frac{b}{d}=\frac{a+b}{c+d}=\frac{a-b}{c-d}\Rightarrow\frac{a+b}{a-b}=\frac{c+d}{c-d}\)
Cách 1:
Ta có:
Cách 2:
Từ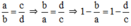
hay