Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét ΔABC có
AD là đường phân giác ứng với cạnh BC
nên \(\dfrac{AB}{AC}=\dfrac{BD}{CD}\)
\(\Leftrightarrow\dfrac{AB}{AC}=\dfrac{3}{4}\)
hay \(AB=\dfrac{3}{4}AC\)
Ta có: BD+CD=BC
nên BC=17,5cm
Áp dụng định lí Pytago vào ΔBAC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow AC^2\cdot\dfrac{25}{16}=\dfrac{1225}{4}\)
\(\Leftrightarrow AC^2=196\)
hay AC=14cm
\(\Leftrightarrow AB=\dfrac{3}{4}AC=10.5\left(cm\right)\)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔBAC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(\left\{{}\begin{matrix}AH\cdot BC=AB\cdot AC\\AB^2=BH\cdot BC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AH=8.4\left(cm\right)\\BH=6.3\left(cm\right)\end{matrix}\right.\)

BÀI 1:
a)
· Trong ∆ ABC, có: AB2= BC.BH
Hay BC= ![]() =
= ![]()
· Xét ∆ ABC vuông tại A, có:
AB2= BH2+AH2
↔AH2= AB2 – BH2
↔AH= ![]() =4 (cm)
=4 (cm)
b)
· Ta có: HC=BC-BH
àHC= 8.3 - 3= 5.3 (cm)
· Trong ∆ AHC, có:

· ![]()
Bài 1:
a) Áp dụng hệ thức lượng ta có:
\(AB^2=BH.BC\)
\(\Rightarrow\)\(BC=\frac{AB^2}{BH}\)
\(\Rightarrow\)\(BC=\frac{5^2}{3}=\frac{25}{3}\)
Áp dụng Pytago ta có:
\(AH^2+BH^2=AB^2\)
\(\Rightarrow\)\(AH^2=AB^2-BH^2\)
\(\Rightarrow\)\(AH^2=5^2-3^2=16\)
\(\Rightarrow\)\(AH=4\)
b) \(HC=BC-BH=\frac{25}{3}-3=\frac{16}{3}\)
Áp dụng hệ thức lượng ta có:
\(\frac{1}{HE^2}=\frac{1}{AH^2}+\frac{1}{HC^2}\)
\(\Leftrightarrow\)\(\frac{1}{HE^2}=\frac{1}{4^2}+\frac{1}{\left(\frac{16}{3}\right)^2}=\frac{25}{256}\)
\(\Rightarrow\)\(\frac{1}{HE}=\frac{5}{16}\)
\(\Rightarrow\)\(HE=\frac{16}{5}\)

Bài 1 : cho tg ABC vuông ở A đường cao AH , biết AH = 16 CH = 25 . Tính AB,AC, BC, BH
Bài làm :
Áp dụng định lý 2 của hệ thức lượng giác trong tam giác ta có :
\(AH^2=BH.CH=>BH=\dfrac{AH^2}{CH}=\dfrac{16^2}{25}=10,24\left(\text{đ}v\text{dd}\right)\)
=> BC = BH + CH = 25 + 10,24 = 35,24 (dvdd)
Áp dụng định lý 1 của hệ thức lượng giác trong tam giác ta có :
\(AB^2=BH.BC=>AB=\sqrt{\left(10,24.35,24\right)}=\sqrt{360,8576}\left(dv\text{dd}\right)\)
Áp dụng Định lý py- ta - go ta có :
\(BC^2=AB^2+AC^2=>AC=\sqrt{\left(30,24^2-\left(\sqrt{360,8576}\right)^2\right)}=\sqrt{553,6}\left(dv\text{dd}\right)\)

Ta có: BD+CD=BC(D nằm giữa B và C)
nên BC=7,5+10=17,5(cm)
Xét ΔABC có AD là đường phân giác ứng với cạnh BC(gt)
nên \(\dfrac{AB}{AC}=\dfrac{BD}{CD}\)(Tính chất tia phân giác của tam giác)
hay \(\dfrac{AB}{AC}=\dfrac{7.5}{10}=\dfrac{3}{4}\)
\(\Leftrightarrow AB=\dfrac{3}{4}AC\)
Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(AB^2+AC^2=BC^2\)
\(\Leftrightarrow AC^2\cdot\dfrac{25}{16}=17.5^2\)
\(\Leftrightarrow AC=14\left(cm\right)\)
\(\Leftrightarrow AB=\dfrac{3}{4}\cdot AC=\dfrac{3}{4}\cdot14=10,5\left(cm\right)\)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(\left\{{}\begin{matrix}AB\cdot AC=AH\cdot BC\\BH\cdot BC=AB^2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AH\cdot17.5=10.5\cdot14\\BH\cdot17.5=10.5^2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}AH=8,4\left(cm\right)\\BH=6,3\left(cm\right)\end{matrix}\right.\)

\(BC=BD+CD=17,5\left(cm\right)\)
Áp dụng định lý phân giác:
\(\dfrac{AB}{AC}=\dfrac{BD}{CD}=\dfrac{3}{4}\Rightarrow AB=\dfrac{3}{4}AC\)
Áp dụng Pitago:
\(AB^2+AC^2=BC^2\Leftrightarrow\left(\dfrac{3}{4}AC\right)^2+AC^2=\left(17,5\right)^2\)
\(\Leftrightarrow AC^2=196\Rightarrow AC=14\)
\(\Rightarrow AB=10,5\left(cm\right)\)
\(AH.BC=AB.AC\Rightarrow AH=\dfrac{AB.AC}{BC}=8,4\left(cm\right)\)
\(AB^2=BH.BC\Rightarrow BH=\dfrac{AB^2}{BC}=6,3\left(cm\right)\)
\(HD=BD-BH=1,2\left(cm\right)\)
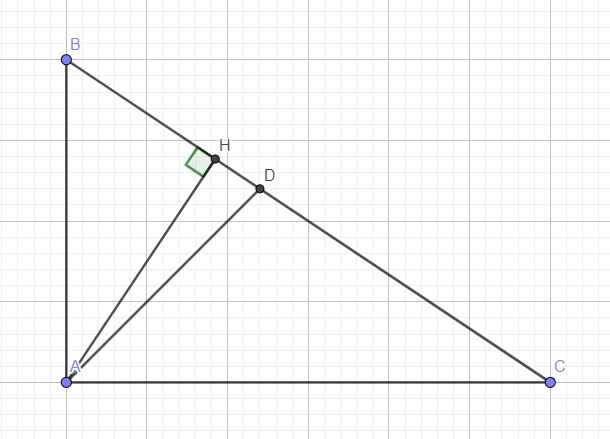
Ta có: BD+CD=BC(D nằm giữa B và C)
nên CD=BC-BD=10-7=3(cm)
Xét ΔABC có AD là đường phân giác ứng với cạnh BC(gt)
nên \(\dfrac{AB}{AC}=\dfrac{BD}{CD}\)(Tính chất đường phân giác)
hay \(\dfrac{AB}{AC}=\dfrac{7}{3}\)
\(\Leftrightarrow AB=\dfrac{7}{3}AC\)
Áp dụng định lí Pytago vào ΔBAC vuông tại A, ta được:
\(AB^2+AC^2=BC^2\)
\(\Leftrightarrow AC=\dfrac{15\sqrt{58}}{29}\)
\(\Leftrightarrow AB=\dfrac{7}{3}\cdot\dfrac{15\sqrt{58}}{29}=\dfrac{35\sqrt{58}}{29}\)
Xét ΔABC vuông tại A có
\(\dfrac{1}{AH^2}=\dfrac{1}{AB^2}+\dfrac{1}{AC^2}\)
\(\Leftrightarrow\dfrac{1}{AH^2}=\dfrac{1}{\left(\dfrac{35\sqrt{58}}{29}\right)^2}+\dfrac{1}{\left(\dfrac{15\sqrt{58}}{29}\right)^2}=\dfrac{841}{11025}\)
\(\Leftrightarrow AH=\dfrac{105}{29}\left(cm\right)\)
Áp dụng định lí Pytago vào ΔAHB vuông tại H, ta được:
\(AB^2=AH^2+BH^2\)
\(\Leftrightarrow BH^2=\dfrac{60025}{641}\)
hay \(BH=\dfrac{245}{29}\left(cm\right)\)
Ta có: BD+DH=BH(D nằm giữa B và H)
nên \(DH=BH-BD\)
\(\Leftrightarrow DH=\dfrac{245}{29}-7=\dfrac{42}{29}\left(cm\right)\)
Vậy: \(AH=\dfrac{105}{29}\left(cm\right)\);\(BH=\dfrac{245}{29}\left(cm\right)\); \(DH=\dfrac{42}{29}\left(cm\right)\)
số xấu thế liệu có đk bn?:))