Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có: BD+CD=BC(D nằm giữa B và C)
nên BC=7,5+10=17,5(cm)
Xét ΔABC có AD là đường phân giác ứng với cạnh BC(gt)
nên \(\dfrac{AB}{AC}=\dfrac{BD}{CD}\)(Tính chất tia phân giác của tam giác)
hay \(\dfrac{AB}{AC}=\dfrac{7.5}{10}=\dfrac{3}{4}\)
\(\Leftrightarrow AB=\dfrac{3}{4}AC\)
Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(AB^2+AC^2=BC^2\)
\(\Leftrightarrow AC^2\cdot\dfrac{25}{16}=17.5^2\)
\(\Leftrightarrow AC=14\left(cm\right)\)
\(\Leftrightarrow AB=\dfrac{3}{4}\cdot AC=\dfrac{3}{4}\cdot14=10,5\left(cm\right)\)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(\left\{{}\begin{matrix}AB\cdot AC=AH\cdot BC\\BH\cdot BC=AB^2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AH\cdot17.5=10.5\cdot14\\BH\cdot17.5=10.5^2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}AH=8,4\left(cm\right)\\BH=6,3\left(cm\right)\end{matrix}\right.\)

\(BC=BD+CD=17,5\left(cm\right)\)
Áp dụng định lý phân giác:
\(\dfrac{AB}{AC}=\dfrac{BD}{CD}=\dfrac{3}{4}\Rightarrow AB=\dfrac{3}{4}AC\)
Áp dụng Pitago:
\(AB^2+AC^2=BC^2\Leftrightarrow\left(\dfrac{3}{4}AC\right)^2+AC^2=\left(17,5\right)^2\)
\(\Leftrightarrow AC^2=196\Rightarrow AC=14\)
\(\Rightarrow AB=10,5\left(cm\right)\)
\(AH.BC=AB.AC\Rightarrow AH=\dfrac{AB.AC}{BC}=8,4\left(cm\right)\)
\(AB^2=BH.BC\Rightarrow BH=\dfrac{AB^2}{BC}=6,3\left(cm\right)\)
\(HD=BD-BH=1,2\left(cm\right)\)
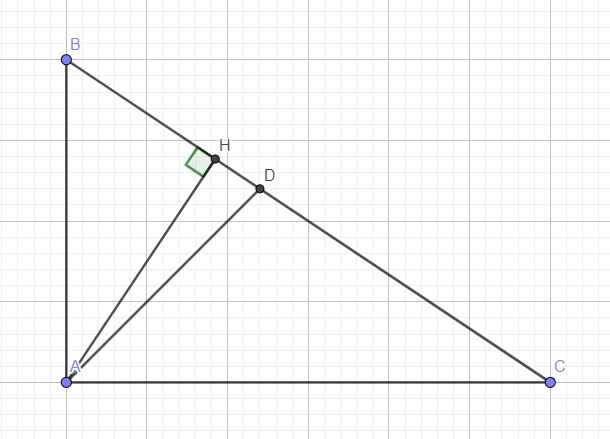
cho tam giác abc vuông tại a, đường cao ah phân giác ad
biết bd =7,5cm; cd=10cm. Tính độ dài ah,bh,hd


Xét ΔABC có
AD là đường phân giác ứng với cạnh BC
nên \(\dfrac{AB}{AC}=\dfrac{BD}{CD}\)
\(\Leftrightarrow\dfrac{AB}{AC}=\dfrac{3}{4}\)
hay \(AB=\dfrac{3}{4}AC\)
Ta có: BD+CD=BC
nên BC=17,5cm
Áp dụng định lí Pytago vào ΔBAC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow AC^2\cdot\dfrac{25}{16}=\dfrac{1225}{4}\)
\(\Leftrightarrow AC^2=196\)
hay AC=14cm
\(\Leftrightarrow AB=\dfrac{3}{4}AC=10.5\left(cm\right)\)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔBAC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(\left\{{}\begin{matrix}AH\cdot BC=AB\cdot AC\\AB^2=BH\cdot BC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AH=8.4\left(cm\right)\\BH=6.3\left(cm\right)\end{matrix}\right.\)

f(x) = (x2 + x + 1)(x2 + x + 2) – 12
Đặt x2 + x + 1 = y ![]() x2 + x + 2 = y + 1
x2 + x + 2 = y + 1
f(x) = y(y + 1) – 12
= y2 + y – 12
= y2 – 3y + 4y – 12
= y(y – 3) + 4(y – 3)
= (y – 3)(y + 4)
Thay y = x2 + x + 1 , ta được:
f(x) = (x2 + x – 2)(x2 + x + 5)
Đến đây ta phân tích tiếp:
x2 + x – 2 = x2 – x + 2x – 2
= x(x – 1) + 2(x – 1)
= (x – 1)(x + 2)
x2 + x + 5 = x2 + x + 
Vì  nên
nên 
Và x2 +x + 5 không thể phân tích được nữa.
Kết quả: f(x) = (x –1)(x + 2)(x2 + x +5).

BÀI 1:
a)
· Trong ∆ ABC, có: AB2= BC.BH
Hay BC= ![]() =
= ![]()
· Xét ∆ ABC vuông tại A, có:
AB2= BH2+AH2
↔AH2= AB2 – BH2
↔AH= ![]() =4 (cm)
=4 (cm)
b)
· Ta có: HC=BC-BH
àHC= 8.3 - 3= 5.3 (cm)
· Trong ∆ AHC, có:

· ![]()
Bài 1:
a) Áp dụng hệ thức lượng ta có:
\(AB^2=BH.BC\)
\(\Rightarrow\)\(BC=\frac{AB^2}{BH}\)
\(\Rightarrow\)\(BC=\frac{5^2}{3}=\frac{25}{3}\)
Áp dụng Pytago ta có:
\(AH^2+BH^2=AB^2\)
\(\Rightarrow\)\(AH^2=AB^2-BH^2\)
\(\Rightarrow\)\(AH^2=5^2-3^2=16\)
\(\Rightarrow\)\(AH=4\)
b) \(HC=BC-BH=\frac{25}{3}-3=\frac{16}{3}\)
Áp dụng hệ thức lượng ta có:
\(\frac{1}{HE^2}=\frac{1}{AH^2}+\frac{1}{HC^2}\)
\(\Leftrightarrow\)\(\frac{1}{HE^2}=\frac{1}{4^2}+\frac{1}{\left(\frac{16}{3}\right)^2}=\frac{25}{256}\)
\(\Rightarrow\)\(\frac{1}{HE}=\frac{5}{16}\)
\(\Rightarrow\)\(HE=\frac{16}{5}\)