D
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
PT
1
LV
1
KK
19 tháng 4 2017
\(tan2a=tan\left[\left(a+b\right)+\left(a-b\right)\right]=\dfrac{tan\left(a+b\right)+tan\left(a-b\right)}{1-tan\left(a+b\right)tan\left(a-b\right)}\)
\(\Rightarrow\dfrac{tan\left(a+b\right)+tan\left(a-b\right)}{1-tan\left(a+b\right)tan\left(a-b\right)}=\dfrac{5+4}{1-5.4}=-\dfrac{9}{19}\)
Vậy \(tan2a=-\dfrac{9}{19}\)
CM
15 tháng 2 2017
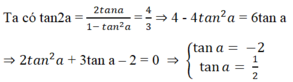
Vì π/2 < a < π nên tan a < 0, do đó tan a = -2.
Áp dụng công thức
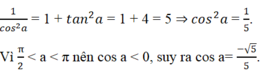
Đáp án là B.
PT
1
CM
6 tháng 5 2018
Chọn B.
Theo công thức cộng ta có:
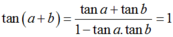
Mà a và b là các góc nhọn suy ra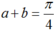 
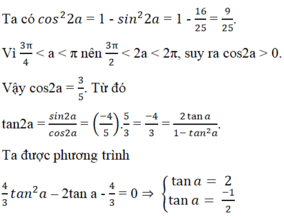
PT
1
CM
2 tháng 2 2017
Vì 3π/4 < a < π nên tan a < 0. Vậy tan a = (-1)/2. Đáp án là D.
NV
Nguyễn Việt Lâm
Giáo viên
4 tháng 3 2021
\(tana-cota=2\sqrt{3}\Rightarrow\left(tana-cota\right)^2=12\)
\(\Rightarrow\left(tana+cota\right)^2-4=12\Rightarrow\left(tana+cota\right)^2=16\)
\(\Rightarrow P=4\)
\(sinx+cosx=\dfrac{1}{5}\Rightarrow\left(sinx+cosx\right)^2=\dfrac{1}{25}\)
\(\Rightarrow1+2sinx.cosx=\dfrac{1}{25}\Rightarrow sinx.cosx=-\dfrac{12}{25}\)
\(P=\dfrac{sinx}{cosx}+\dfrac{cosx}{sinx}=\dfrac{sin^2x+cos^2x}{sinx.cosx}=\dfrac{1}{sinx.cosx}=\dfrac{1}{-\dfrac{12}{25}}=-\dfrac{25}{12}\)
24 tháng 5 2020
gợi ý tan 10o = cot 80o
mà tan a . cot a =1
phần còn lại tự làm
chưa hiểu thì hỏi nhé
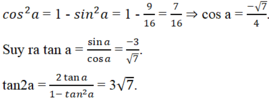
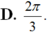
\(tan\left(a+b\right)=7;tan\left(a-b\right)=4\)
\(tan2a=tan\left[\left(a+b\right)+\left(a-b\right)\right]=\dfrac{7+4}{1-7.4}=\dfrac{11}{-27}=-\dfrac{11}{27}\)