NT
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
TG
3 tháng 3 2021
Ta có: \(\left\{{}\begin{matrix}\dfrac{AD}{AB}=\dfrac{2AB}{AB}=2\\\dfrac{AE}{AC}=\dfrac{2AC}{AC}=2\end{matrix}\right.\Rightarrow\dfrac{AD}{AB}=\dfrac{AE}{AC}\)
Xét tam giác ADE và tam giác ABC ta có:
\(\dfrac{AD}{AB}=\dfrac{AE}{AC}\left(cmt\right)\)
Góc DAE = Góc BAC (đối đỉnh)
\(\Rightarrow\Delta ADE\sim\Delta ABC\left(c-g-c\right)\)
\(\Rightarrow\dfrac{AD}{AB}=\dfrac{ED}{BC}=\dfrac{AE}{AC}\)
17 tháng 7 2017
xét tam giác EAD và tam giác ABC có:
-AD=AB
- góc EAD= góc BAC
-AE=EC
Ta suy ra tam giác EAD = tam giác ABC (c-g-c)
=> góc EDA= góc ABC
mà 2 góc này pử vị trí so le trong
=> ED//AB
=>BCDE LÀ HÌNH THANG
Q
23 tháng 3 2017
Có: tam giác ABC đồng dạng với tam giác ADE
=>AB/AD=AC/AE
Có AB/AD=AB/2AB=1/2
AC/AE=AC/2AC=1/2
Vậy tam giác ABC đồng dạng với tam giác ADE the tỉ số đồng dạng là 1/2
14 tháng 8 2019
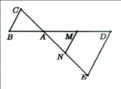
( Hình tự vẽ nha )
Ta có : AB = AE ( gt )
AD = AC ( gt )
Do đó : AB + AD = AC + AE
=> BD = EC
=> Tứ giác BDEC là hình thang ( vì trong hình thang có hai đường chéo bàng nhau )
Do AD = 2AB \(\Rightarrow\frac{AD}{2AB}=\frac{1}{2}.\frac{AD}{AB}=1\) (1)
Do \(AE=2AC\Rightarrow\frac{AE}{2AC}=\frac{1}{2}.\frac{AE}{AC}=1\) (2)
Từ 1 và 2 suy ra \(\frac{AD}{AB}=\frac{AE}{AC}\)
xét tam giác ADE và tam giác ABC có :
A1 =A2 ( 2 góc đối đỉnh)
\(\frac{AD}{AB}=\frac{AE}{AC}\)
suy ra tam giác ADE đồng dạng tam giác ABC ( c.g.c)
b)Ta có
\(\frac{\Delta ADE}{\Delta ABC}=\frac{AD}{AB}=\frac{AE}{AC}=\frac{2AB}{AB}=\frac{2AC}{AC}=2\) ( tính chất 2 tam giác đồng dạng)
Vậy tỉ số đồng dạng của tam giác ADE và tam giác ABC là 2