Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

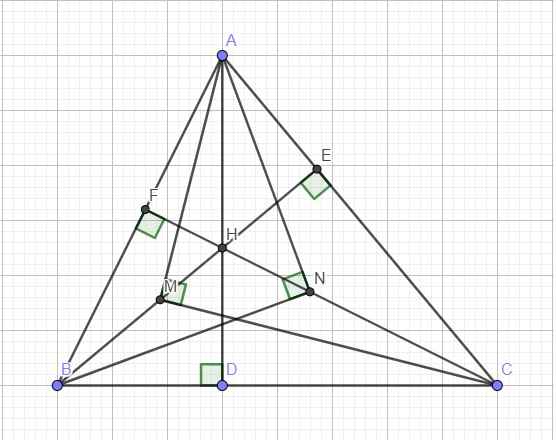
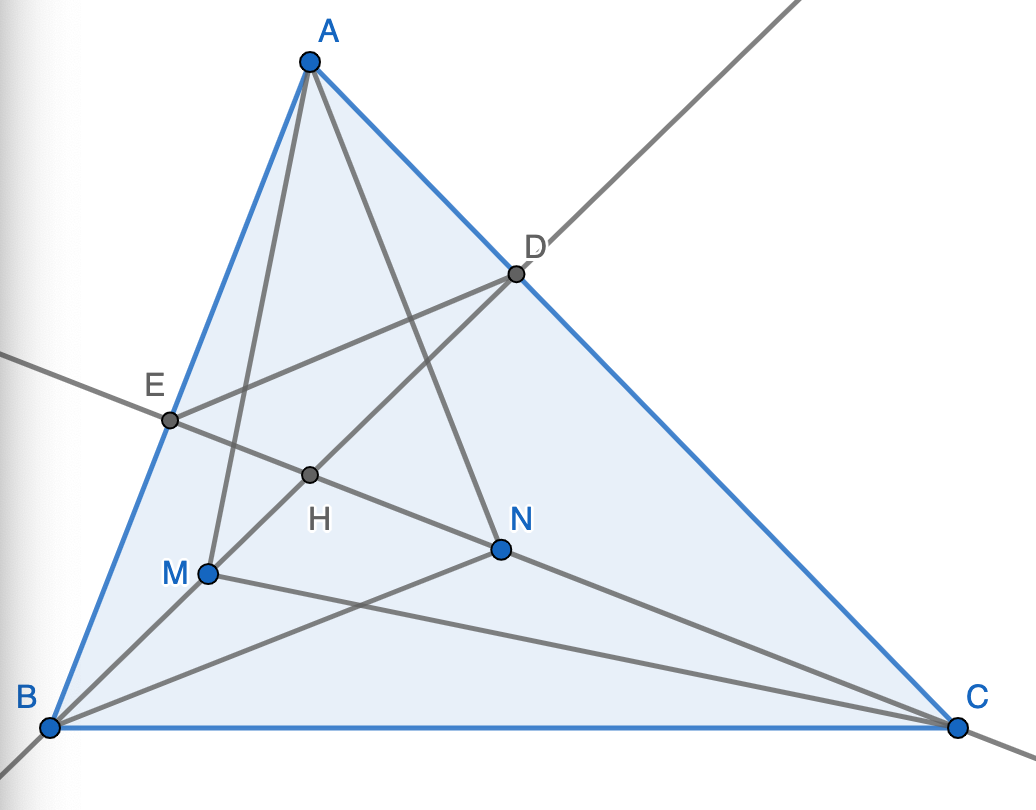
Theo đề có: `ΔAMC` là Δ vuông, đường cao `MD`.
=> `AM^2=AD.AC` (1)
`ΔANB` là Δ vuông, đường cao `NE`:
=> `AN^2=AE.AB` (2)
Lại có: `ΔABD=ΔACE`(g.g)
=> \(\dfrac{AB}{AC}=\dfrac{AD}{AE}\Leftrightarrow AB.AE=AC.AD\left(3\right)\)
Từ (1), (2), (3) suy ra: `AM=AD` (đpcm)
$HaNa$

Tính chất cơ bản của tam giác với 3 đường cao: \(\Delta AEF\sim\Delta ABC\) (bài toán quen thuộc chắc em tự c/m được)
\(\Rightarrow AF.AB=AE.AC\)
Trong tam giác vuông ABN với đường cao NF:
\(AN^2=AF.AB\)
Trong tam giác vuông ACM:
\(AM^2=AE.AC\)
\(\Rightarrow AM^2=AN^2\Rightarrow AM=AN\)
b. Hệ thức lượng: \(BN^2=BF.AB\) ; \(CM^2=CE.AC\)
\(\Delta ABD\sim\Delta CBF\) (2 tam giác vuông chung góc B)
\(\Rightarrow\dfrac{AB}{BC}=\dfrac{BD}{BF}\Rightarrow BF.AB=BD.BC\) (1)
Hoàn toàn tương tư, \(\Delta ADC\sim\Delta BEC\Rightarrow CE.AC=CD.BC\) (2)
Cộng vế (1) và (2) \(\Rightarrow BF.AB+CE.AC=\left(BD+CD\right)BC=BC^2\)
\(\Rightarrow BN^2+CM^2=BC^2\)
\(\Rightarrow BN.CM\le\dfrac{1}{2}\left(BN^2+CM^2\right)=\dfrac{1}{2}BC^2=2a^2\)
Dấu "=" xảy ra khi tam giác cân tại A

Do: Góc ABD = Góc ACE (= 90 - A)
=> Δ ABD ∼ Δ ACE (2 Δ vuông)
=> AD.AC = AE.AB (tỉ lệ đồng dạng)
<=> AM2 = AN2 (Hệ thức lượng trong Δ vuông)
<=> AM = AN
Hay Δ AMN cân tại A.=>....

Trong t/g vuông ANB có NE là đường cao: AN^2 = AE.AB
Trong t/g vuông AMC có MD là đường cao: AM^2 = AD.AC
Mà t/g ABD ~ t/g ACE (g.g) nên AB/AC = AD/AE <=> AB.AE = AC.AD
=> AN^2 = AM^2 <=> AN = AM