Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

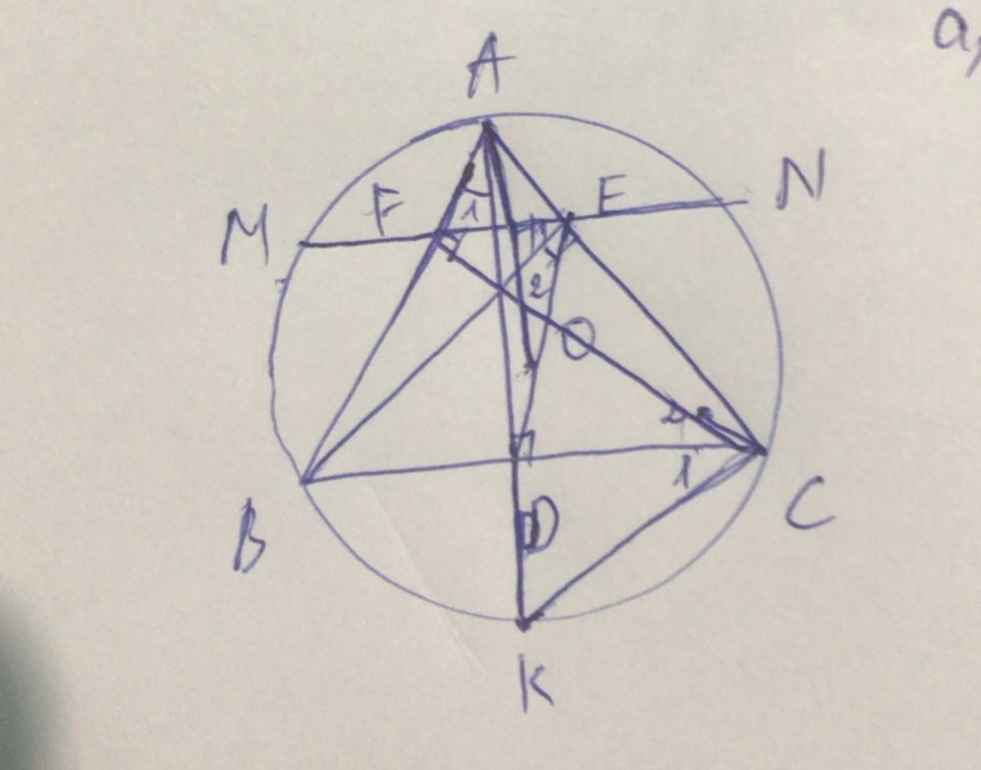
a) Xét tứ giác BFEC có
\(\widehat{BFC}=\widehat{BEC}\left(=90^0\right)\)
nên BFEC là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)
Xét ΔAEB vuông tại E và ΔAFC vuông tại F có
\(\widehat{BAE}\) chung
Do đó: ΔAEB\(\sim\)ΔAFC(g-g)
Suy ra: \(\dfrac{AE}{AF}=\dfrac{AB}{AC}\)
hay \(AE\cdot AC=AB\cdot AF\)

Gọi G là giao điểm của FC và AK.
Áp dụng định lý Menelaus cho tam giác FBC với cát tuyến A, G, K ta có:
\(\dfrac{AF}{AB}.\dfrac{KB}{KC}.\dfrac{GC}{GF}=1\Rightarrow\dfrac{GC}{GF}=\dfrac{KC}{KB}.\dfrac{AB}{AF}\). (1)
Áp dụng định lý Menelaus cho tam giác ACB với cát tuyến K, E, F ta có:
\(\dfrac{EA}{EC}.\dfrac{KC}{KB}.\dfrac{FB}{FA}=1\Rightarrow\dfrac{KC}{KB}=\dfrac{FA}{FB}.\dfrac{EC}{EA}\). (2)
Từ (1), (2) có \(\dfrac{GC}{GF}=\dfrac{EC}{EA}.\dfrac{AB}{FB}\). (*)
Mặt khác áp dụng định lý Menelaus cho tam giác AFC với cát tuyến B, H, E ta có:
\(\dfrac{HC}{HF}.\dfrac{BF}{BA}.\dfrac{EA}{EC}=1\Rightarrow\dfrac{HC}{HF}=\dfrac{AB}{FB}.\dfrac{EC}{EA}\). (**)
Từ (*), (**) ta có \(\dfrac{GC}{GF}=\dfrac{HC}{HF}\Rightarrow\dfrac{AC}{MF}=\dfrac{AC}{NF}\Rightarrow FM=FN\).




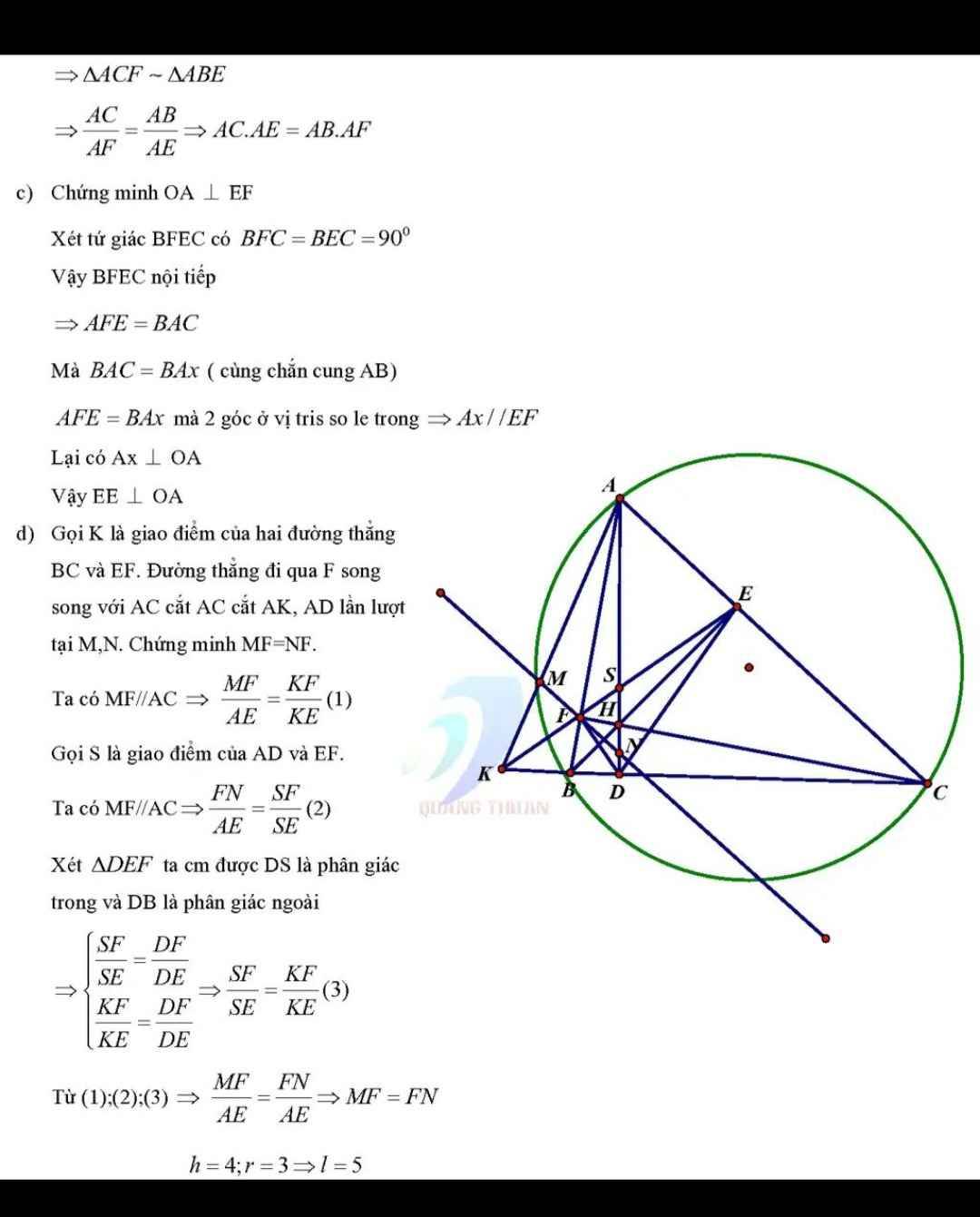
Tứ giác FEAH có: \(\widehat{FAH}=\widehat{AEH}=90^o\)
=> Tứ giác FEAH nội tiếp => \(\widehat{HEF}=\widehat{FAH}\)
Tứ giác ABDE có: \(\widehat{ADB}=\widehat{AEB}=90^o\)
=> Tứ giác ABDE nội tiếp => \(\widehat{BAD}=\widehat{BED}\)
Vậy \(\widehat{HEF}=\widehat{BED}\)
Xét \(\Delta\)HIE \(\left(\widehat{HIE}=90^o\right)\)và \(\Delta\)HKE \(\left(\widehat{HKE}=90^o\right)\)có:
EH chung
\(\widehat{HEI}=\widehat{HEK}\)
=> \(\Delta HIE=\Delta HKE\) (cạnh huyền-góc nhọn)
=> \(\hept{\begin{cases}EI=EK\\HI=HK\end{cases}}\)(2 cạnh tương ứng)
=> \(\Delta\)KEI cân tại E, \(\Delta\)HIK cân tại H
\(\Rightarrow\widehat{KIE}=\frac{1}{2}\widehat{IEK}\Rightarrow\widehat{KIE}+\widehat{FAH}=90^o\)
Mà \(\widehat{MHF}=\widehat{FAH}=90^o\)
Do đó: \(\widehat{KIE}=\widehat{MHF}\)=> Tứ giác FIMH nội tiếp => \(\widehat{MHF}=\widehat{HIF}=90^o\)
Tứ giác HMNK có: \(\widehat{HMN}=\widehat{HKN}=90^o\)=> Tứ giác HMNK nội tiếp
Ta có: \(\hept{\begin{cases}\widehat{HFN}=\widehat{HIK}\\\widehat{HNM}=\widehat{HIK}\\\widehat{HIK}=\widehat{HKI}\end{cases}}\)
=> \(\Delta\)HFN đồng dạng \(\Delta\)HIK (g.g)
=> \(\frac{HF}{HI}=\frac{HN}{HK},HI=HK\Rightarrow HF=HN\)
\(\Delta\)HFN cân tại H, HM _|_ FN => HM là đường trung tuyến của tam giác HFN
FM _|_ AD, BD _|_ AD => FM//BD
MF=MN, DB=DC nên \(\frac{AM}{AD}=\frac{MN}{DS}\)
Xét \(\Delta\)AMN và \(\Delta\)ADS có:
\(\widehat{AMN}=\widehat{ADS}\left(MN//BS\right),\frac{AM}{AD}=\frac{MN}{DS}\)
=> \(\Delta\)AMN đồng dạng \(\Delta\)ADS (c.g.c)
=> \(\widehat{MAN}=\widehat{DAS}\)
=> 2 tia AN, AS trùng nhau => A,N,S thẳng hàng