K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

10 tháng 5 2023
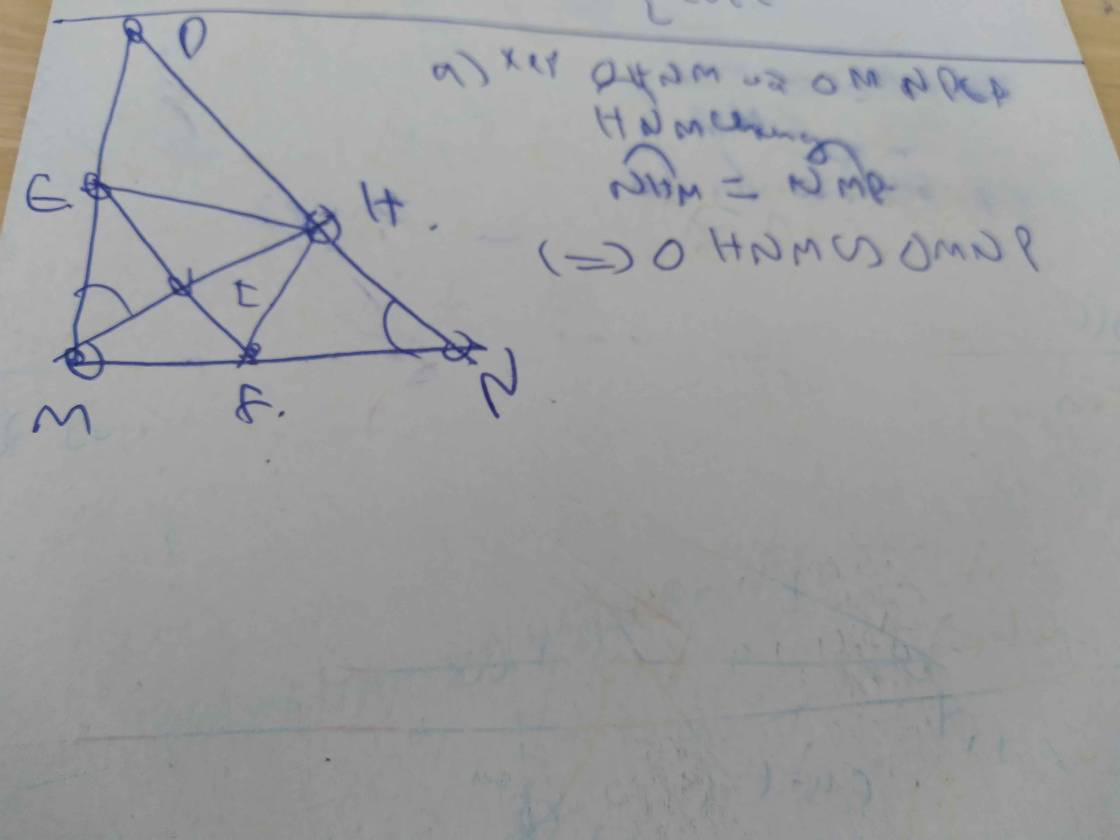
a: Xét ΔHNM vuông tại H và ΔMNP vuông tại M có
góc N chung
=>ΔHNM đồng dạng với ΔMNP
b: ΔMNP vuông tại M co MH vuông góc NP
nên MH^2=HN*HP

18 tháng 9 2021
\(ME=MF\Rightarrow M\in\) đường trung trực của EF\((1)\)
\(ME=MF;MN=MP\left(GT\right)\\ \Rightarrow MN-ME=MP-MF\\ \Rightarrow NE=FP\)
Tam giác MNP cân tại M có MH là đường cao nên cũng là trung tuyến
\(\left\{{}\begin{matrix}NE=PF\\\widehat{ENH}=\widehat{FPH}\left(\Delta MNP.cân.tại.M\right)\\NH=HP\end{matrix}\right.\Rightarrow\Delta NEH=\Delta PFH\left(c.g.c\right)\\ \Rightarrow EH=FH\)
\(\Rightarrow H\in\) trung trực của EF\((2)\)
\(\left(1\right)\left(2\right)\Rightarrow MH\) là trung trực của EF
Vậy E đối xứng F qua MH
a) Trong trường hợp \(MN=6cm,MP=8cm\) thì \(S_{MNP}=\frac{1}{2}MN.MP=24\left(cm^2\right)\)
b) Xét \(\Delta NHM\) và \(\Delta MHP\): \(\widehat{NHM}=\widehat{MHP}=90^0,\widehat{HMN}=\widehat{HPM}=90^0-\widehat{HMP}\)
Suy ra \(\Delta NHM~\Delta MHP\). Vậy \(\frac{HN}{HM}=\frac{HM}{HP}\Leftrightarrow HM^2=HN.HP.\)
c) Vì \(\widehat{HNF}=\widehat{HME}=90^0-\widehat{HMN}\)
\(\widehat{HFN}=180^0-\widehat{MFH}=180^0-\left(360^0-2.90^0-\widehat{HEM}\right)=\widehat{HEM}\)
Nên \(\Delta HFN~\Delta HEM\), suy ra \(\frac{HN}{HF}=\frac{HM}{HE}\). Do đó \(\Delta EHF~\Delta MHN.\)
d) Gọi \(G\) là hình chiếu vuông góc của \(H\) trên \(MP.\)
Từ kết quả của ý c, ta có \(\frac{S_{EHF}}{S_{MHN}}=\frac{HE^2}{HM^2}\ge\frac{HG^2}{HM^2}\Leftrightarrow S_{EHF}\ge\frac{HG^2}{HM^2}S_{MHN}\) (không đổi)
Dấu "=" xảy ra khi \(E\equiv G.\)