Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔMIN vuông tại I và ΔMQP vuông tại Q có
góc M chung
=>ΔMIN đồng dạng với ΔMQP
c: Xét ΔMQI và ΔMPN có
MQ/MP=MI/MN
góc M chung
=>ΔMQI đồng dạng với ΔMPN

1: Xét ΔMEN vuông tại E và ΔMFP vuông tại F có
\(\widehat{EMN}\) chung
Do đó: ΔMEN~ΔMFP
2: Xét ΔHFN vuông tại F và ΔHEP vuông tại E có
\(\widehat{FHN}=\widehat{EHP}\)(hai góc đối đỉnh)
Do đó: ΔHFN~ΔHEP
3: Ta có; ΔMEN~ΔMFP
=>\(\dfrac{ME}{MF}=\dfrac{MN}{MP}\)
=>\(\dfrac{ME}{MN}=\dfrac{MF}{MP}\)
Xét ΔMEF và ΔMNP có
\(\dfrac{ME}{MN}=\dfrac{MF}{MP}\)
\(\widehat{EMF}\) chung
Do đó: ΔMEF~ΔMNP
4: Ta có: ΔHFN~ΔHEP
=>\(\dfrac{HF}{HE}=\dfrac{HN}{HP}\)
=>\(\dfrac{HF}{HN}=\dfrac{HE}{HP}\)
Xét ΔHFE và ΔHNP có
\(\dfrac{HF}{HN}=\dfrac{HE}{HP}\)
\(\widehat{FHE}=\widehat{NHP}\)(hai góc đối đỉnh)
Do đó: ΔHFE~ΔHNP

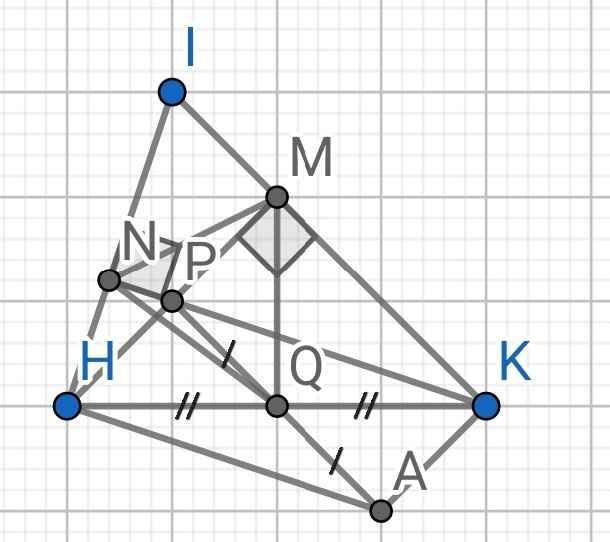 a) Do PQ = QA (gt)
a) Do PQ = QA (gt)
⇒ Q là trung điểm của AP
Tứ giác PHAK có:
Q là trung điểm của AP (cmt)
Q là trung điểm của HK (gt)
⇒ PHAK là hình bình hành
b) Do PHAK là hình bình hành (cmt)
⇒ PK = AH
c) ∆HNK vuông tại N
Q là trung điểm của HK (gt)
⇒ NQ là đường trung tuyến ứng với cạnh huyền HK
⇒ NQ = HK : 2 (1)
∆HMK vuông tại M
Q là trung điểm HK (gt)
⇒ MQ là đường trung tuyến ứng với cạnh huyền HK
⇒ MQ = HK : 2 (2)
Từ (1) và (2) ⇒ MQ = NQ
∆MNQ có:
MQ = NQ (cmt)
⇒ ∆MNQ cân tại Q

Trong 1 tam giác, 3 đường phân giác cắt nhau tại 1 điểm và điểm đó cách đều 3 cạnh của tam giác (điểm này gọi là tâm đường tròn nộ tiếp). Nối E -> F; E -> D ; D -> F. Ta sẽ chứng minh H là giao điểm 3 đường phân giác.
Ta chứng minh được ∆AFC ~ ∆AEB(g.g) => AF/AE = AC/AB => AF/AC = AE/AB. => ta chứng minh được ∆AEF ~ ∆ABC(c.g.c) => góc AEF = góc ABC, chứng minh tương tư ta được ∆CED ~ ∆CBA => góc CED = góc ABC => góc AEF = góc CED ( = góc ABC), ta có: góc FEB = 90º - góc AEF và góc BED = 90º - góc CED, mà góc AEF = góc CED => góc FEB = góc BED => BE là phân giác góc FED => EH là phân giác góc FED, chứng minh tương tự ta được DH là phân giác góc EDF và FH là phân giác góc EFD
=> đpcm
bạn chứng minh rõ DH là tia phân giác cho mình đc k, k rõ cho lắm
