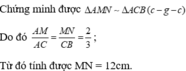Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
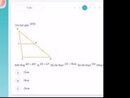
Xét ΔAFH có
DE//FH
Do đó: \(\dfrac{DE}{FH}=\dfrac{AD}{AF}\)
\(\Leftrightarrow FH=2DE\)
Xét hình thang BDEC có
F là trung điểm của BD
FH//ED//BC
Do đó: H là trung điểm của EC
Xét hình thang BDEC có
F là trung điểm của BD
H là trung điểm của EC
Do đó: FH là đường trung bình của hình thang BDEC
Suy ra: \(FH=\dfrac{DE+BC}{2}\)
\(\Leftrightarrow DE=2\left(cm\right)\)
hay FH=4(cm)
Lời giải:
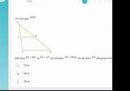
Theo đề thì AB là đường trung bình ứng với đáy NP của tam giác $MNQ$.
$\Rightarrow AB=\frac{NP}{2}=\frac{18}{2}=9$ (cm)
Xét tam giác ABC và MN//BC
Hai tam giác AMN và ABC, có:
- góc AMN = góc ABC (đồng vị)
- góc ANM = góc ACB (đồng vị)
- BAC là góc chung
Mặt khác, theo hệ quả định lí Ta-lét, hai tam giác AMN và ABC có 3 cặp cạnh tương ứng tỉ lệ:
\(\frac{AM}{AB}=\frac{MN}{BC}=\frac{AN}{AC}\)
Nên tam giác AMN đồng dạng với tam giác ABC
\(\Rightarrow\frac{AM}{AB}=\frac{AN}{AC}=\frac{1}{3}\)
\(\Rightarrow\frac{AN}{18}=\frac{1}{3}\)
\(AN=\frac{18.1}{3}=6\)
Do AC = AN + NC
\(\Rightarrow NC=AC-AN=18-6=12\)
Vậy NC có độ dài là 12 cm
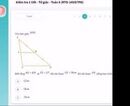
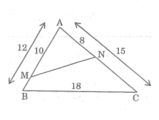
Ta có: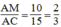 
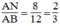
Suy ra: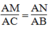 
Xét ΔABC và ΔANM, ta có
+ Góc A chung
+ 
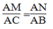
Suy ra:
△
ANM đồng dạng
△
ABC(c.g.c) ⇒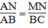 
Vậy MN =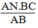 
= (8.18)/12 = 12 cm