Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A. \(\sin A = \sin \,(B + C)\)
Ta có: \((\widehat A + \widehat C) + \widehat B= {180^o}\)
\(\Rightarrow \sin \,(B + C) = \sin A\)
=> A đúng.
B. \(\cos A = \cos \,(B + C)\)
Sai vì \(\cos \,(B + C) = - \cos A\)
C. \(\;\cos A > 0\) Không đủ dữ kiện để kết luận.
Nếu \({0^o} < \widehat A < {90^o}\) thì \(\cos A > 0\)
Nếu \({90^o} < \widehat A < {180^o}\) thì \(\cos A < 0\)
D. \(\sin A\,\, \le 0\)
Ta có \(S = \frac{1}{2}bc.\sin A > 0\). Mà \(b,c > 0\)
\( \Rightarrow \sin A > 0\)
=> D sai.
Chọn A

A. \({a^2} = {b^2} + {c^2} + \sqrt 2 ab.\) (Loại)
Vì: Theo định lí cos ta có: \({a^2} = {b^2} + {c^2} - 2bc.\cos A\)
Không đủ dữ kiện để suy ra \({a^2} = {b^2} + {c^2} + \sqrt 2 ab.\)
B. \(\frac{b}{{\sin A}} = \frac{a}{{\sin B}}\) (Loại)
Theo định lí sin, ta có: \(\frac{a}{{\sin A}} = \frac{b}{{\sin B}} \nRightarrow \frac{b}{{\sin A}} = \frac{a}{{\sin B}}\)
C. \(\sin B = \frac{{ - \sqrt 2 }}{2}\)(sai vì theo câu a, \(\sin B = \frac{{\sqrt 2 }}{2}\))
D. \({b^2} = {c^2} + {a^2} - 2ca\cos {135^o}.\)
Theo định lý cos ta có:
\({b^2} = {c^2} + {a^2} - 2ca.\cos B\) (*)
Mà \(\widehat B = {135^o} \Rightarrow \cos B = \cos {135^o}\).
Thay vào (*) ta được: \({b^2} = {c^2} + {a^2} - 2ca\;\cos {135^o}\)
=> D đúng.
Chọn D

Theo định lí sin, ta có: \(\frac{a}{{\sin A}} = \frac{b}{{\sin B}} = \frac{c}{{\sin C}} = 2R\)
=> \(R = \frac{a}{{2\sin A}}\) => A sai.
\(R = \frac{b}{{2\sin B}}=\frac{b}{{2\sin 135^o}}=\frac{{\sqrt 2 }}{2}b\) => B đúng.
C. \(R = \frac{{\sqrt 2 }}{2}c\) (Loại vì không có dữ kiện về góc C nên không thể tính R theo c.)
D. \(R = \frac{{\sqrt 2 }}{2}a\) (Loại vì không có dữ kiện về góc A nên không thể tính R theo a.)
Chọn B

Theo định lí sin trong tam giác ta có: a sin A = 2 R ⇒ a = 2 R . sin A
Tương tự, b = 2RsinB; c= 2R.sin C
Theo đầu bài:
a + b =2c ⇒ 2Rsin A + 2Rsin B = 4Rsin C ⇒ sin A + sin B = 2sin C.
ĐÁP ÁN C

\(\Rightarrow C\\ \Leftrightarrow a^2=b^2+c^2-2b.c.cos\left(120\right)=b^2+c^2-2bc\dfrac{-1}{2}\\ =b^2+c^2+bc\)

Câu 5:
D. Các vector \(\overrightarrow{AB}, \overrightarrow{BA}, \overrightarrow{AC}, \overrightarrow{CA}, \overrightarrow{BC}, \overrightarrow{CB}\)

Ta có: b . cos C + c . cos B = b . a 2 + b 2 − c 2 2 a b + c . c 2 + a 2 − b 2 2 a c
= a 2 + b 2 − c 2 2 a + c 2 + a 2 − b 2 2 a = a 2 + b 2 − c 2 + c 2 + a 2 − b 2 2 a = 2 a 2 2 a = a
ĐÁP ÁN B

* Diện tích tam giác ABC là: S = 1 2 b c . sin A ⇒ 4 S = 2 b c sin A
cot A = cosA sin A = b 2 + c 2 − a 2 2 b c sin A = b 2 + c 2 − a 2 2 b c . s i n A = b 2 + c 2 − a 2 4 S
* Tương tự, ta có: cot B = a 2 + c 2 − b 2 4 S ; cot C = a 2 + b 2 − c 2 4 S
* Do đó,
cot A + cot B + cot C = b 2 + c 2 − a 2 4 S + a 2 + c 2 − b 2 4 S + a 2 + b 2 − c 2 4 S = a 2 + b 2 + c 2 4 S
ĐÁP ÁN B

Đáp án A
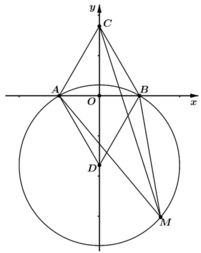
Chọn hệ trục Oxy sao cho Ox trùng với AB , chiều dương hướng từ A đến B ,trục Oy là đường trung trực của đoạn AB =>
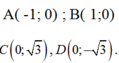
Phương trình đường tròn tâm D qua A; B là:
![]()
Giả sử M(a;b) là điểm bất kì trên đường tròn .Ta có :
MA2= (a+ 1) 2+ b2
MB2= (a-1) 2+ b2
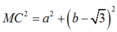

+ M nằm trên đường tròn (1) nên : 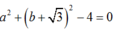
=> MA2+ MB2= MC2
=> MA; MB; MC là độ dài ba cạnh của một tam giác vuông.

Theo định lí sin trong tam giác ta có:
a sin A = 2 R ⇒ a = 2 R . sin A
Tương tự, b = 2 R . sin B ; c = 2 R . sin C
Ta có: a b = c 2 n ê n 2 R . sin A . 2 R . sin B = ( 2 R sin C ) 2
Hay sin A . sin B = ( sin C ) 2
ĐÁP ÁN A
Đáp án D