Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

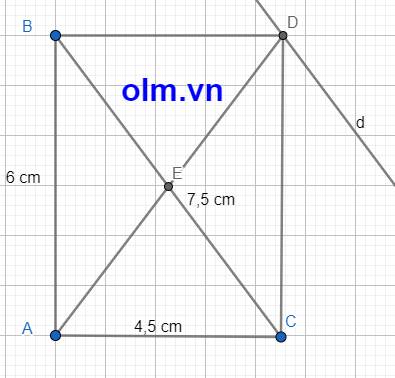
a, Xét \(\Delta\)ABC có: AB2 + AC2 = 62 + 4,52 = 56,25 (cm2)
BC2 = 7,52 = 56,25 (cm2)
AB2 + AC2 = BC2 vậy tam giác ABC vuông tại A (đpcm)
SinC = 6 : 7,5 =0,8 ⇒ \(\widehat{C}\) = 53,130 ⇒ \(\widehat{B}\) = 900 - 53,130 = 36,870
b, Dựng hình chữ nhật ABCD, chiều cao AH, DK, và đường thẳng d đi qua D song song với BC như hình vẽ ta có
SABC = SBDC ⇒ AH = DK
Lây 1 điểm bất M kỳ di động trên đường thẳng d ta có:
SBDC = SMBC (vì hai tam giác có chiều cao bằng nhau và chung cạnh đáy BC)
⇒ SABC = SMBC
Kết luận khi M di động trên đường thẳng d thì diện tích tam giác MBC luôn bằng diện tích tam giác ABC

Vì \(AM\perp AH\left(gt\right)\)(1)
và \(BC\perp AH\left(gt\right)\)(2)
Từ(1) và (2)
\(\Rightarrow AM//BC\)(T/c )
Mà \(EF//BC\)(* )
Do \(\widehat{AEF}=\widehat{ABC}\)(do vị trí đồng vị )'
\(\Rightarrow AH\perp EF\)(*)
Mà \(AM\perp AH\left(gt\right)\)(** )
Từ (*) và (** )
\(\Rightarrow AM\perp EF\)
( đpcm)


a: Xét ΔOAM vuông tại A có cosAOM=OA/OM=1/2
nên góc AOM=60 độ
=>góc AOB=60 độ
=>sđ cung AB=60 độ
b: Xét (O) có
MA,MC là tiếp tuyến
nên MA=MC
mà OA=OC
nên OM là trung trực của AC
=>OM vuông góc với AC
c: Xét ΔOAB có OA=OB và góc AOB=60 độ
nên ΔOAB đều
mà AH là đườg cao
nên H là trung điểm của OB
=>HO=HB
Vì MO là trung trực của AC
nên MO vuông góc AC tại H và H là trung điểm của AC
HA*HC=HA^2
HO*HM=HA^2
=>HA*HC=HO*HM
=>HA*HC=HB*HM
d: Xét ΔOBC có OB=OC và góc BOC=60 độ
nên ΔBCO đều
=>OB=OC=BC=OA=AB
=>OA=AB=BC=OC
=>OABC là hình thoi