Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
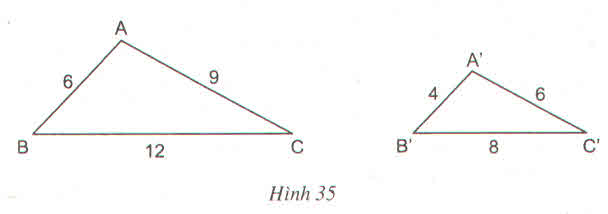
ABA′B′ABA′B′ = BCB′C′BCB′C′= CAC′A′CAC′A′= 3/2
=> ∆ABC ∽ ∆A'B'C'
b) CABCCA′B′C′CABCCA′B′C′= 3/2
a)Xét \(\Delta ABC\) và \(\Delta A'B'C'\) có:
\(\dfrac{AB}{A'B'}=\dfrac{BC}{B'C'}=\dfrac{AC}{A'C'}\)
\(\Rightarrow\Delta ABC\)∽\(\Delta A'B'C'\)(c.c.c)
b)Từ câu a và áp dụng tính chất tỉ lệ thức ta có:
\(\dfrac{AB}{A'B'}=\dfrac{BC}{B'C'}=\dfrac{AC}{A'C'}=\dfrac{AB+BC+AC}{A'B'+B'C'+A'C'}=\dfrac{3}{2}\)
mà \(C_{ABC}=AB+BC+AC\)
\(C_{A'B'C'}=A'B'+B'C'+A'C'\)
Vậy tỉ số chu vi của \(\Delta ABC\) và \(\Delta A'B'C'\)là:
\(\dfrac{C_{ABC}}{C_{A'B'C'}}=\dfrac{3}{2}\)
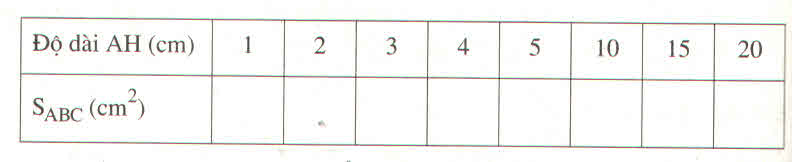
a:
| AH | 1 | 2 | 3 | 4 | 5 | 10 | 15 | 20 |
| S | 2 | 4 | 6 | 8 | 10 | 20 | 30 | 40 |
b: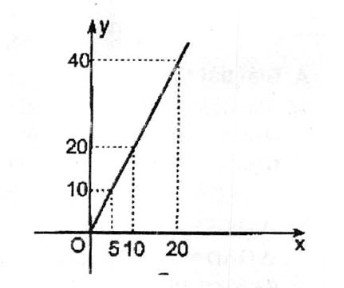 
c: Diện tích tam giác tỉ lệ thuận với chiều cao
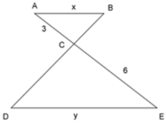
Ta có: ΔABC ~ ΔEDC
A B E D = A C E C ⇔ x y = 4 6 = 2 3
Đáp án: B
\(\frac{x+1}{7}+\frac{x+2}{6}=\frac{x+3}{5}+\frac{x+4}{4}\)
\(\Leftrightarrow\left(\frac{x+1}{7}+1\right)+\left(\frac{x+2}{6}+1\right)=\left(\frac{x+3}{5}+1\right)+\left(\frac{x+4}{4}+1\right)\)
\(\Leftrightarrow\frac{x+8}{7}+\frac{x+8}{6}-\frac{x+8}{5}-\frac{x+8}{4}=0\)
\(\Leftrightarrow\left(x+8\right).\left(\frac{1}{7}+\frac{1}{6}-\frac{1}{5}-\frac{1}{6}\right)=0\)
\(\Leftrightarrow x+8=0\) ( do \(\left(\frac{1}{7}+\frac{1}{6}-\frac{1}{5}-\frac{1}{6}\right)\ne0\))
\(\Leftrightarrow x=-8\)
Vậy x = - 8
Bài này của lp 7 mà _________ Cách trình bày của lp 7
@@ Học tốt
Chiyuki Fujito
\(\frac{x+1}{7}+1+\frac{x+2}{6}+1=\frac{x+3}{5}+1+\frac{x+4}{4}+1\)
\(\frac{x+8}{7}+\frac{x+8}{6}=\frac{x+8}{5}+\frac{x+4}{4}\)
\(\left(x+8\right).\left(\frac{1}{7}+\frac{1}{6}-\frac{1}{4}-\frac{1}{5}\right)=0\)
\(x+8=0\)
\(x=-8\)
DÚP MK VS NHÉ! 
MK CẦN GẮP LÉM Ạ!
THANKS MẤY BN DÚP MK NHỀU NHỀU NHÂN!
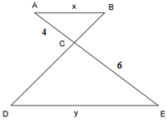
Ta có: ΔABC ~ ΔEDC
⇒ A B E D = A C E C ⇔ x y = 3 6 = 1 2
Đáp án: B