Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a, Xet tam giac CDE co :
KC=KD va CI=IE
=> KI la tdb
=> KI=1/2DE va KI//DE (1)
Xet tam giac
Xét tam giác DOE co :
DM=MO va ON=NE
=>MN la tdb
=> MN=1/2 DE va MN//DE (2)
Từ(1)(2) suy ra : MNIK la HBH
b, Xét tam giác CDO co :
KC=KD
DM=MO
=> KM là dtb tam giác CDO
=> KM=1/2 OC
Va KM//OC
=> KM vuông góc với MN =>M=90
Mà trong hình bình hành có một góc vuông là hình chữ nhật
Vậy O là phải thỏa mãn diện kiến là trực tâm (giao điểm của 3 đường cao) đệ tứ giác MNIK là hình chữ nhật .

a. Vì M,N là trung điểm AB,AC nên MN là đtb tg ABC
Do đó BC=2MN=5(cm)
b. Vì MN là đtb tg ABC nên \(MN=\dfrac{1}{2}BC;MN\text{//}BC\left(1\right)\)
Vì I,K là trung điểm MB,MC nên IK là đtb tg MBC
Do đó \(IK=\dfrac{1}{2}BC;IK\text{//}BC\left(2\right)\)
\(\left(1\right)\left(2\right)\Rightarrow MN=IK;MN\text{//}IK\\ \Rightarrow MNIK\text{ là hbh}\)
c. Để MNIK là hcn thì \(MI\bot MN\)
Mà \(MI\equiv AB;MN\text{//}BC\Leftrightarrow AB\bot BC\)
Vậy ABC vuông tại A thì MNIK là hcn
d. Kẻ đường cao AH của tam giác ABC và AMN
Do đó \(\dfrac{S_{ABC}}{S_{AMN}}=\dfrac{\dfrac{1}{2}AH\cdot BC}{\dfrac{1}{2}AH\cdot MN}=\dfrac{BC}{MN}=2\)
\(\Rightarrow S_{AMN}=\dfrac{1}{2}S_{ABC}=\dfrac{a}{2}\)

a) HS tự chứng minh
b) O nằm trên đường cao xuất phát từ đỉnh A của DABC
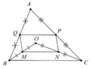

a) N đối xứng với I qua P => NP vuông góc với AB => Góc NPB = 90
CMTT: Góc NQB = 90
Xét tứ giác BPNQ có 3 góc vuông => BPNQ là hình chữ nhật.
b) BPNQ là hình chữ nhật => PN = BQ = IN (I đối xứng với N qua P) ; BP = QN = QK (N đối xứng với K qua Q)
Xét tam giác IPB và tam giác BQK có IP = BQ, BP = KQ, góc IPB = góc BQK = 90
=> Hai tam giác bằng nhau => IBP = BKQ , BIP = KBQ, IB = KB
Góc IBK = IBP + PBQ + QBK = 90 + 90 = 180
=> I, B, K thẳng hàng ; mà IB = BK => B là trung điểm IK
c) BPNQ là hình vuông => BP = PN = NQ = QB <=> 2BP = 2PN = 2NQ = 2QB <=> AB = BC
Vậy tam giác ABC vuông cân tại B thì BPNQ là hình vuông.
d) Gọi giao điểm của AK và BN là O. Ta cần c/m : CI cắt BN tại O
Xét tứ giác ANKB có AB = NK (= 2PB) , AB // NK (PB // NQ)
=> ABKN là hình bình hành => AK cắt BN tại trung điểm của mỗi đường <=> O là trung điểm BN
CMTT ta có INCB ;à hình bình hành => IC cắt BN tại trung điểm của mỗi đường => IC cắt BN tại O
=> AK, BN, CI đồng quy tại O

Bài khá dài đó.
Sorry nhé mik mới lớp 6 ak nên ko bít, tha lỗi nha!
ý kiến gì thì nhắn tin cho mik mai 7g
pp, ngủ ngon!

a: Xét ΔABD có
M là trung điểm của AB
K là trung điểm của AD
Do đó: MK là đường trung bình của ΔBAD
Suy ra: MK//BD và \(MK=\dfrac{BD}{2}\left(1\right)\)
Xét ΔCBD có
N là trung điểm của BC
I là trung điểm của CD
Do đó: NI là đường trung bình của ΔCBD
Suy ra: NI//BD và \(NI=\dfrac{BD}{2}\left(2\right)\)
Từ (1) và (2) suy ra MK//NI và MK=NI
hay MKIN là hình bình hành
Việt Nam nói là làm( phải tích tui đúng xong tui trả lời thui ak)