Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔADE có AD=AE
nên ΔADE cân tại A
c: Xét ΔABC có
AD/AB=AE/AC
Do đó: DE//BC

a, Xét ABE và ACD có :
AB = AC(gt)
^A - chung
AE = AD (gt)
=> ABE = ACD (c.g.c)
=> BE=CD ( 2 cạnh tương ứng)
b,vì tam giác MBD= tam giác MEC:
=> DM=EM ( 2 cạnh đồng vị)
XÉt tam giác AMD và tam giác AME
AD =AE ( Gt)
DM=EM ( CMT)
AM cạnh chung
=> tam giác AMD=AME ( c.c.c )
chúc bạn học tốt

a: Xét ΔABC co AD/AB=AE/AC
nên DE//BC
b: Xét ΔDBM và ΔECM có
DB=EC
góc B=goc C
BM=CM
=>ΔDBM=ΔECM
b: Xét ΔADM và ΔAEM có
AD=AE
AM chung
MD=ME
=>ΔAMD=ΔAME

a: Xét ΔABM vuông tại M và ΔACM vuông tại M có
AB=AC
AM chung
Do đó: ΔABM=ΔACM
b: Xét ΔABE và ΔACD có
AB=AC
\(\widehat{BAE}\) chung
AE=AD
Do đó: ΔABE=ΔACD
Xét ΔABC có \(\dfrac{AD}{AB}=\dfrac{AE}{AC}\)
nên DE//BC
c: Ta có: AD+DB=AB
AE+EC=AC
mà AD=AE và AB=AC
nên DB=EC
Xét ΔDBC và ΔECB có
DB=EC
\(\widehat{DBC}=\widehat{ECB}\)
BC chung
Do đó: ΔDBC=ΔECB
=>\(\widehat{DCB}=\widehat{EBC}\)
=>\(\widehat{IBC}=\widehat{ICB}\)
=>ΔIBC cân tại I
Xét ΔAIB và ΔAIC có
AI chung
IB=IC
AB=AC
Do đó: ΔAIB=ΔAIC
=>\(\widehat{BAI}=\widehat{CAI}\)
=>AI là phân giác của góc BAC

a, Xét \(\Delta\)ABE và \(\Delta\)ACD cs :
AB = AC(gt)
^A - chung
AE = AD (gt)
=> \(\Delta\)ABE = \(\Delta\)ACD (c.g.c)
b) Từ \(\Delta\)ABE = \(\Delta\)ACD (câu a)
=> đpcm
a) Xét \(\Delta ABE\)và \(\Delta ACD\)có:
\(AB=AC\left(gt\right)\)
\(\widehat{A}\)là góc chung
\(AD=DE\left(gt\right)\)
\(\Rightarrow\Delta ABE=\Delta ACD\left(c.g.c\right)\)
\(\Rightarrow BE=CD\)( 2 cạnh tương ứng )
b) Đề sai, điểm M đâu???
c) Ta có: \(AD=AE\left(gt\right)\)
\(\Rightarrow\Delta ADE\)cân tại A
\(\Rightarrow\widehat{ADE}=\frac{180^0-\widehat{DAE}}{2}\left(1\right)\)
Lại có: \(\Delta ABC\)cân tại A ( gt )
\(\Rightarrow\widehat{ABC}=\frac{180^0-\widehat{DAE}}{2}\left(2\right)\)
Từ (1) và (2) \(\Rightarrow\widehat{ADE}=\widehat{ABC}\)
mà 2 góc này ở vị trí đồng vị
\(\Rightarrow DE//BC\left(đpcm\right)\)

a: Xét ΔABC có AD/AB=AE/AC
nên DE//BC
b: Xét ΔABE và ΔACD có
AB=AC
góc A chung
AE=AD
=>ΔABE=ΔACD
c: Xét ΔIDB và ΔIEC có
góc IDB=góc IEC
DB=EC
góc IBD=góc ICE
=>ΔIDB=ΔIEC
d: Xét ΔABI và ΔACI có
AB=AC
BI=CI
AI chung
=>ΔABI=ΔACI
=>góc BAI=góc CAI
=>AI là phân giác của góc BAC

a: Xét ΔABE và ΔACDcó
AB=AC
góc BAE chung
AE=AD
=>ΔABE=ΔACD
=>BE=CD
b: ΔABE=ΔACD
=>góc ABE=góc ACD
c: góc ABE+góc KBC=góc ABC
góc ACD+góc KCB=góc ACB
mà góc ABE=góc ACD và góc ABC=góc ACB
nên góc KBC=góc KCB
=>KB=KC
d: AB=AC
KB=KC
=>AK là trung trực của BC
=>A,K,I thẳng hàng

Tham khảo:
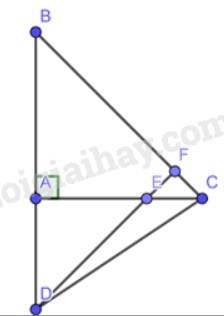
a) Vì tam giác ABC vuông cân tại A
\( \Rightarrow \) \(\widehat B = \widehat C = {45^o}\)(2 góc ở đáy bằng nhau)
Xét tam giác AED có :
AE = AD
AC vuông góc với AB
\( \Rightarrow \) Tam giác AED vuông cân tại A
\( \Rightarrow \widehat {ADE} = \widehat {AED} = {45^o}\)
Mà \(\widehat {AED};\widehat {CEF}\)là 2 góc đối đỉnh \( \Rightarrow \widehat {AED} = \widehat {CEF} = {45^o}\)
Xét tam giác CEF áp dụng định lí tổng 3 góc trong tam giác ta có :
\( \Rightarrow \widehat F + \widehat C + \widehat E = {180^o}\)
\( \Rightarrow \widehat F = {180^o} - {45^o} - {45^o} = {90^o} \Rightarrow EF \bot BC \Rightarrow DE \bot BC\)
b) Vì DE vuông góc với BC \( \Rightarrow \) DE là đường cao của tam giác BCD
Vì AC cắt DE tại E nên E là trực tâm tam giác BCD (Do AC cũng là đường cao của tam giác BCD)
\( \Rightarrow \)BE cùng là đường cao của tam giác BCD (định lí 3 đường cao trong tam giác đi qua trực tâm)
\( \Rightarrow \)BE vuông góc với DC
Nguyễn Thuỳ Linh Hình như bài này t lm cho c r mà nhỉ
( Hình tự vẽ )
a) +) Xét \(\Delta\)ABE và \(\Delta\)ACD có
AB = AC ( gt)
\(\widehat{BAC}\) : góc chung
AE = AD ( gt)
=> \(\Delta\)ABE = \(\Delta\)ACD (c-g-c)
b) Theo câu a ta có \(\Delta\)ABE = \(\Delta\)ACD
=> BE = CD ( 2 cạnh tương ứng )
c) +) Xét \(\Delta\) ABC cân tại A
=> \(\widehat{ABC}=\frac{180^o-\widehat{A}}{2}\) (1) ( tính chất tam giác cân )
+) Xét \(\Delta\)AED có AE = AD ( gt)
=> \(\Delta\)AED cân tại A
=> \(\widehat{AED}=\frac{180^o-\widehat{A}}{2}\) (2) ( tính chất tam giác cân )
Từ (1) và (2) \(\Rightarrow\widehat{ABC}=\widehat{AED}\)
Mà 2 góc này ở vị trí đồng vị
=> ED // BC
@@ Hc tốt
Takigawa Miu_