Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Gọi O là trung điểm của MC
=>O là tâm đường tròn đường kính MC
Xét (O) có
ΔCNM nội tiếp
CM là đường kính
Do đó: ΔCNM vuông tại N
=>MN\(\perp\)NC tại N
=>MN\(\perp\)CB tại N
Xét tứ giác ABNM có \(\widehat{MNB}+\widehat{MAB}=90^0+90^0=180^0\)
nên ABNM là tứ giác nội tiếp
=>A,B,N,M cùng thuộc một đường tròn
b: ABNM là tứ giác nội tiếp
=>\(\widehat{ANM}=\widehat{ABM}\)
=>\(\widehat{ANM}=\widehat{ABI}\)(1)
Xét tứ giác CIAB có \(\widehat{CIB}=\widehat{CAB}=90^0\)
nên CIAB là tứ giác nội tiếp
=>\(\widehat{ABI}=\widehat{ACI}\)
mà \(\widehat{ACI}=\widehat{MCI}=\widehat{MNI}\left(=\dfrac{1}{2}sđ\stackrel\frown{MI}\right)\)
nên \(\widehat{ABI}=\widehat{MNI}\left(2\right)\)
Từ (1) và (2) suy ra \(\widehat{MNI}=\widehat{MNA}\)
=>NM là phân giác của góc ANI

Gọi N là điểm đối xứng với C qua F. Ta có EF = NE + NF = BC/2 = BE + CF = BE + NF, suy ra B và N đối xứng qua E
Lại có \(CP.CA=CF.CB=\frac{CN}{2}.2CM=CM.CN\). Do vậy 4 điểm A,P,M,N đồng viên
Hoàn toàn tương tự A,Q,M,N đồng viên. Từ đó 5 điểm A,M,N,P,Q đồng viên hay 4 điểm A,M,P,Q đồng viên (đpcm).


a, HS tự chứng minh
b, HS tự chứng minh
c, Chứng minh được: B A M ^ = M B C ^
Từ đó chứng minh được:
∆MAB:∆MBD => M B 2 = M A . M D

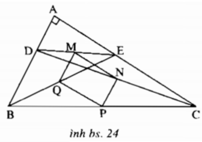
Xét ΔCDB có CN/CD=CP/CB
nên NP//BD và NP=DB/2
Xét ΔEDB có EM/ED=EQ/EB
nên MQ//BD và MQ=BD/2
=>NP//MQ và NP=MQ
Xét ΔDEC có DN/DC=DM/DE
nên MN//EC
=>MN vuông góc với AB
=>MN vuông góc với NP
Xét tứ giác MNPQ có
NP//MQ
NP=MQ
MN vuông góc với NP
Do đó: MNPQ là hình chữ nhật
=>M,N,P,Q cùng thuộc 1 đường tròn

Xét ΔCDB có CN/CD=CP/CB
nên NP//BD và NP=DB/2
Xét ΔEDB có EM/ED=EQ/EB
nên MQ//BD và MQ=BD/2
=>NP//MQ và NP=MQ
Xét ΔDEC có DN/DC=DM/DE
nên MN//EC
=>MN vuông góc với AB
=>MN vuông góc với NP
Xét tứ giác MNPQ có
NP//MQ
NP=MQ
MN vuông góc với NP
Do đó: MNPQ là hình chữ nhật
=>M,N,P,Q cùng thuộc 1 đường tròn

a: Xét (O) có
ΔBEC nội tiếp
BC là đường kính
Do đó: ΔBEC vuông tại E
Xét (O) có
ΔBDC nội tiếp
BC là đường kính
Do đó: ΔBDC vuông tại D
Xét ΔABC có
BD là đường cao
CE là đường cao
BD cắt CE tại H
Do đó: AH⊥BC

Từ M kẻ ME vuông góc với AB,MF vuông góc với AC.
Ta có ΔEBM vuông cân tại E, ΔFMC vuông cân tại F và AEMF là hình chữ nhật.
Áp dụng định lý Pytago vào các tam giác EBM,FMC,AEF ta có:
BM^2 = EM^2 + BE^2 = 2.ME^2 ; MC^2 = 2.FM^2 ⇒ BM^2 + MC^2 = 2.(ME^2 + MF^2) (1)
Mà AM^2 = EF^2 = ME^2 + MF^2 (2)
Từ (1),(2) ta được 2AM^2 = MB^2 + MC^2