Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

xét Tam giác HBA và Tam giác ABC có
B Chung
Góc H=A(=90 độ)
=> tam giác HBA Đồng dạng với tam giác giác ABC (g.g)
=> AH/AC=AB/BC
(BC)^2=AB^2+AC^2
BC^2=400
BC=20
AH/AC=AB/BC => AH=AB.AC/BC=16x12/20=9.6

Tự vẽ hình nha
a) xét tam giác HAB và tam giác ABC
góc AHB = góc ABC
góc CAB : chung
Suy ra : tam giác AHB ~ tam giác ABC ( g-g )
b) Áp dụng định lí py - ta - go vào tam giác ABC ta được :
AC2 + AB2 = BC2
162 + 122 = BC2
400 = BC2
=> BC = = 20 ( cm )
ta có tam giác HAB ~ tam giác ABC ( câu a )
=>
=> AH = ( cm )
Độ dài cạnh BH là
Áp dụng định lí py - ta - go vào tam giác HBA ta được :
AH2 + BH2 = AB2
BH2 = AB2 - AH2
BH2 = 122 - 9,62
BH2 = 51,84
=> BH = = 7,2 ( cm )
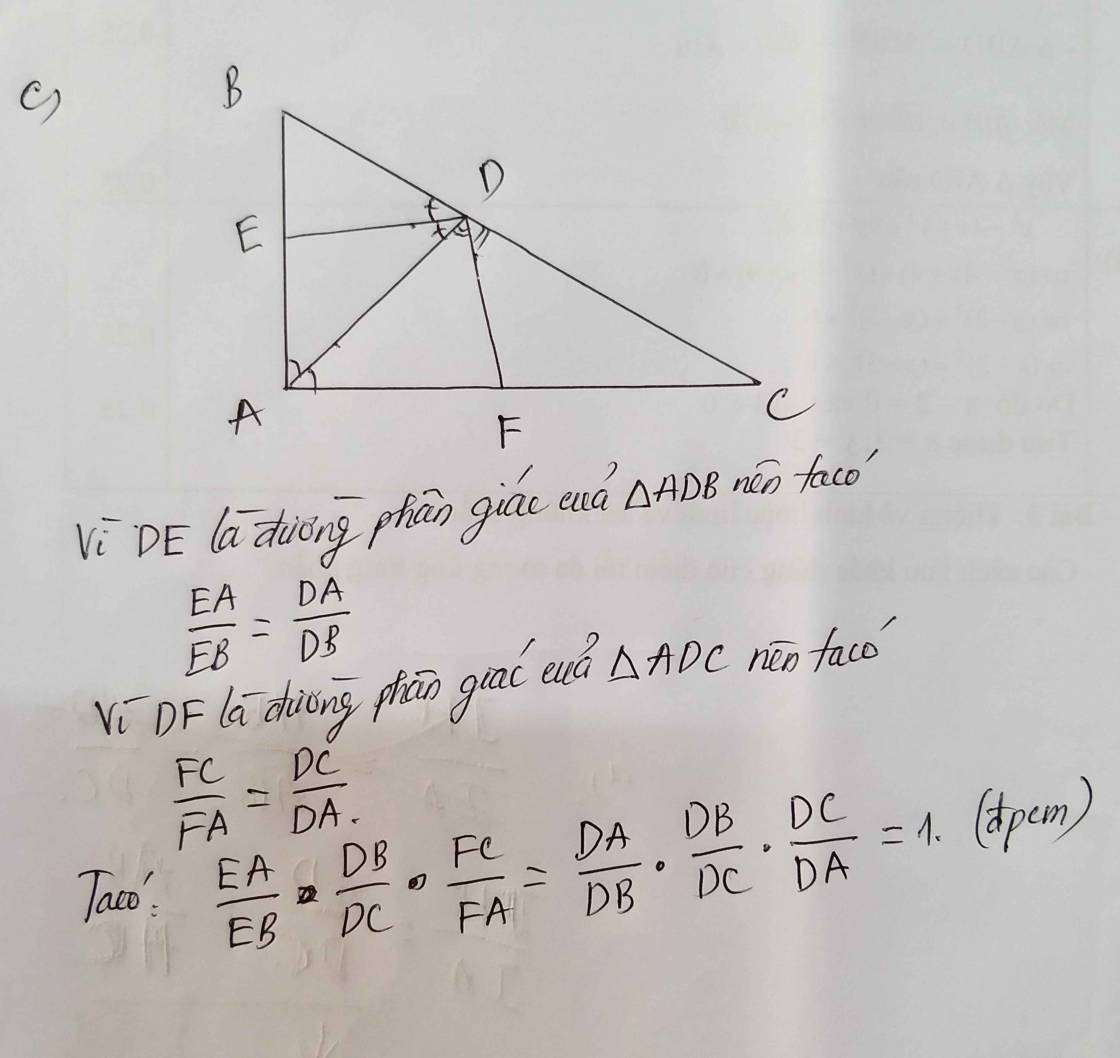
c) Vì AD là đường phân giác của tam giác ABC nên :
<=>
<=> AB.CD = AC(BC - CD)
hay 12CD = 16.20 - 16CD
<=> 12CD+ 16CD = 320
<=> 28CD = 320
<=> CD =
Độ dài cạnh BD là :
BD = BC - CD
BD = 20 - 8,57 ( cm )

xét Tam giác HBA và Tam giác ABC có
B Chung
Góc H=A(=90 độ)
=> tam giác HBA Đồng dạng với tam giác giác ABC (g.g)
=> AH/AC=AB/BC
(BC)^2=AB^2+AC^2
BC^2=400
BC=20
AH/AC=AB/BC => AH=AB.AC/BC=16x12/20=9.6

Sửa đề: ΔABC vuông tại A
a) Xét ΔDAB vuông tại D và ΔACB vuông tại A có
\(\widehat{ABC}\) chung
Do đó: ΔDAB\(\sim\)ΔACB(g-g)
b) Xét ΔABC có
BE là đường phân giác ứng với cạnh AC(gt)
nên \(\dfrac{AE}{EC}=\dfrac{AB}{BC}\)(Định lí đường phân giác của tam giác)(1)
Ta có: ΔDAB\(\sim\)ΔACB(cmt)
nên \(\dfrac{AB}{BC}=\dfrac{BD}{BA}\)(Các cặp cạnh tương ứng tỉ lệ)(2)
Từ (1) và (2) suy ra \(\dfrac{AE}{EC}=\dfrac{BD}{AB}\)
hay \(AE\cdot AB=BD\cdot EC\)(đpcm)

Do bạn SSBĐ Love HT làm được câu a) rồi nên mình làm nốt câu b) còn lại nhé :
a) Ta tính được : \(BC=20cm,BD=DC=10cm\)
b) Do \(\Delta ABC\) vuông ở A, có \(AH\perp BC\)
\(\Rightarrow S_{ABC}=\frac{1}{2}\cdot AB\cdot AC=\frac{1}{2}\cdot AH\cdot BC\)
\(\Leftrightarrow12\cdot16=AH\cdot20\)
\(\Leftrightarrow AH=\frac{48}{5}\left(cm\right)\)
Áp dụng định lý Pytago cho các tam giác vuông ta có :
+) \(\Delta ABH\) vuông tại H \(\Rightarrow AB^2=AH^2+BH^2\)
\(\Leftrightarrow12^2=\left(\frac{48}{5}\right)^2+BH^2\)
\(\Leftrightarrow BH=\frac{36}{5}\left(cm\right)\)
\(\Rightarrow HD=BD-BH=10-\frac{36}{5}=\frac{14}{5}\left(cm\right)\)
+) \(\Delta AHD\) vuông tại H \(\Rightarrow AD^2=AH^2+HD^2\)
\(\Rightarrow AD^2=\left(\frac{48}{5}\right)^2+\left(\frac{14}{5}\right)^2\)
\(\Rightarrow AD=10cm\)
Vậy : \(AH=\frac{48}{5}\left(cm\right),HD=\frac{14}{5}\left(cm\right),AD=10\left(cm\right)\)
a)ΔABC vuông tại A
Áp dụng định lí Pitago:
⇒ BC=\(\sqrt{AB^2+AC^2}=\sqrt{12^2+16^2}=20cm\)
AD là tia phân giác ta có:
\(\frac{AB}{AC}\)=\(\frac{BD}{DC}\)Hay \(\frac{AB}{AC}\)=\(\frac{BD}{BC-BD}\)=\(\frac{12}{16}\)=\(\frac{3}{4}\)
\(\Rightarrow\frac{BD}{20-BD}\)=\(\frac{3}{4}\)\(\rightarrow\)4BD=60-3BD⇒ BD=8\(\times\)6cm
⇒ CD=BC-BD=20-8,6=11,4cm
b)Xét ΔAHB và ΔABC
\(\widehat{CAB}\)là góc chung
\(\widehat{AHB}=\widehat{ABC}\)
⇒ΔAHB đồng dạng ΔABC
\(\frac{AH}{AC}\)=\(\frac{AB}{AC}\)
⇒AH=\(\frac{AC\times AB}{BC}\)=\(\frac{16-12}{20}\)=\(9,6cm\)
Áp dụng hệ thức lượng : BH=\(\frac{36}{5}\);\(CH=\frac{64}{5}\)
⇒ HD=BD-BH=8\(\times\)6−\(\frac{36}{5}\)=1,4cm
ΔDHA vuông tại H
⇒AD=\(\sqrt{AH^2+HD^2}=\sqrt{9\times6^2+1\times4^2}=9,7cm\)
Đáp án:a)BC=20cm; BD=8.6cm; CD=11,4cm
b)AH=9.6cm; HD=1.4cm; AD=9.7cm