Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Xét tam giác BMN và tam giác CMA , có :
MB = MC ( gt )
MN = MA ( gt )
góc BMN = góc CMA ( đối đỉnh )
=> tam giác BMN = tam giác CMA ( c-g-c )
=> BN = CA ( hai cạnh tương ứng )
=> góc BNM = góc CAM ( hai góc tương ứng ) mà hai góc ở vị trí so le trong nên AC // BN ( dấu hiệu nhận biết hai đường thẳng song song )
Vậy BN = CA ; AC // BN ( đpcm )
b) Vì AC // BN nên AB ; CN vuông góc với BN hay góc ABN = 90o
Vậy góc ABN = 90o
c) Xét tam giác ABC và tam giác BAN , có :
BA : chung
AC = BN ( tam giác BMN = tam giác CMA )
góc CAB = góc NBA ( = 90o )
=> tam giác ABC = tam giác BAN ( hai cạnh góc vuông )
Vậy tam giác ABC = tam giác BAN ( hai cạnh góc vuông )
d) Vì tam giác ABC = tam giác BAN ( chứng minh câu c ) => BC = AN ( hai cạnh tương ứng ) mà AM = 1/2 AN => AM = 1/2 BC
Vậy AM = 1/2 BC

a) Xét ΔMAB và ΔMKC có
MA=MK(gt)
\(\widehat{AMB}=\widehat{KMC}\)(hai góc đối đỉnh)
MB=MC(M là trung điểm của BC)
Do đó: ΔMAB=ΔMKC(c-g-c)

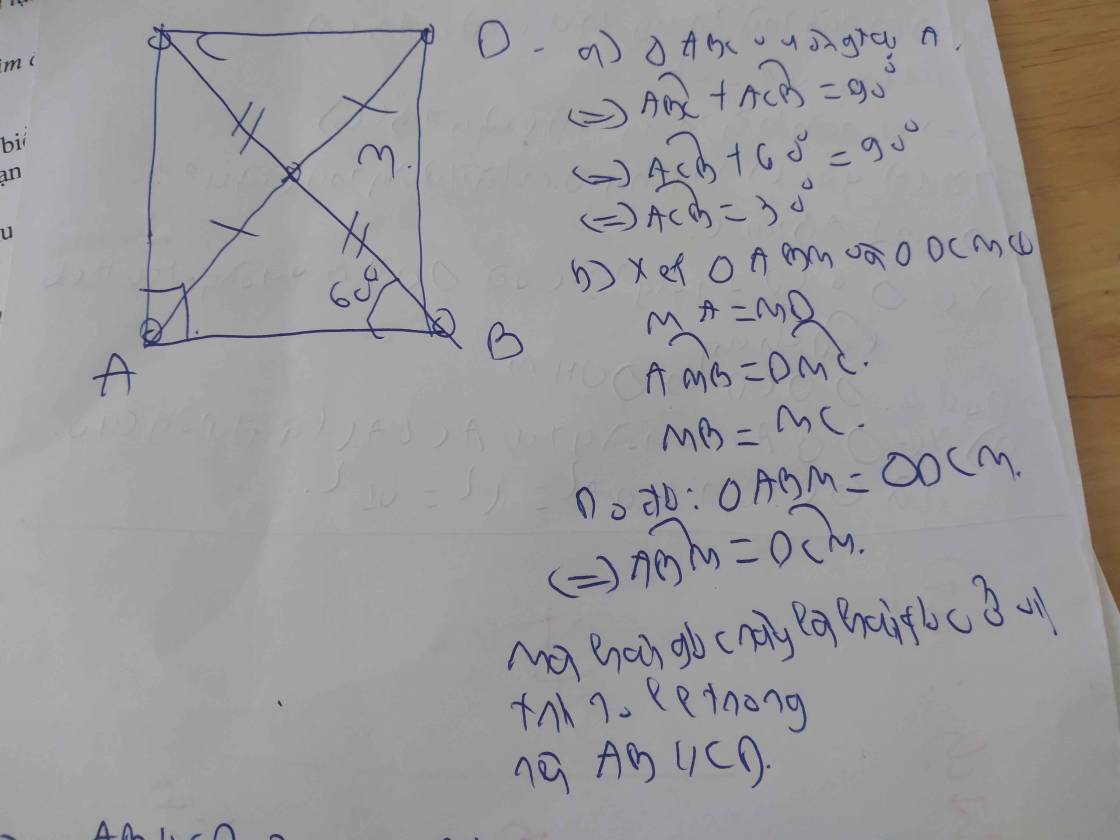
a, Ta có \(\widehat{ABC}+\widehat{ACB}=90^0\Rightarrow3\widehat{ACB}=90^0\Rightarrow\left\{{}\begin{matrix}\widehat{ACB}=30^0\\\widehat{ABC}=60^0\end{matrix}\right.\)
b, Vì \(\left\{{}\begin{matrix}BM=MC\\AM=MD\\\widehat{AMC}=\widehat{BMD}\left(đối.đỉnh\right)\end{matrix}\right.\) nên \(\Delta ACM=\Delta DBM\left(c.g.c\right)\)
c, Vì \(\left\{{}\begin{matrix}AC=BD\left(\Delta ACM=\Delta DBM\right)\\AB.chung\\BC=AD\left(=2AM\right)\end{matrix}\right.\) nên \(\Delta ABC=\Delta BAD\left(c.c.c\right)\)
Do đó \(\widehat{BAC}=\widehat{ABD}=90^0\)
Vậy ...


a: Xét tứ giác ABNC có
M là trung điểm của BC
Mlà trung điểm của AN
Do đó: ABNC là hình bình hành
mà \(\widehat{BAC}=90^0\)
nên ABNC là hình chữ nhật
Suy ra: BN=AC vàBN//AC
b: Ta có: ABNC là hình chữ nhật
nên \(\widehat{ABN}=90^0\)
c: Xét ΔABC và ΔBAN có
AB chung
BC=AN
AC=BN
Do đo: ΔABC=ΔBAN
d: Ta có: ΔABC vuông tại A
mà AM là đường trung tuyến
nên AM=1/2BC