Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A B C K H I
a/ Ta có
\(AB\perp AC\left(gt\right)\)
\(HK\perp AC\left(gt\right)\)
=> AB//HK (cùng vuông góc với AC)
b/ Xét tg AKI có
\(AH\perp HI\) => AH là đường cao của tg AKI
HK=HI (gt) => AH là trung tuyến của tg AKI
=> tg AKI cân tại A (Tam giác có đường cao đồng thời là đường trung tuyến thì tg đó là tg cân)
c/ Ta có
tg AKI cân tại A \(\Rightarrow\widehat{AIK}=\widehat{AKI}\) (góc ở đáy tg cân)
AB//HK (cmt) \(\Rightarrow\widehat{BAK}=\widehat{AKI}\) (góc so le trong)
\(\Rightarrow\widehat{BAK}=\widehat{AIK}\) (cùng bằng góc \(\widehat{AKI}\) )
d/ Xét tg CKI có
\(CH\perp KI\) => CH là đường cao của tg CKI
HK=HI => CH là trung tuyến của tg CKI
=> tg CKI cân tại C (Tam giác có đường cao đồng thời là đường trung tuyến thì tg đó là tg cân)
Xét tg AIC và tg AKC có
tg AKI cân tại A (cmt) => AI=AK
tg CKI cân tại C (cmt) => CI=CK
AC chung
=> tg AIC = tg AKC (c.c.c)

A B C H K I
mk vẽ ko có kí hiệu bn thông cảm
a) dễ thấy AB // HK ( vì cùng vuông góc với AC)
b) Vì \(AC\perp KI\)tại H và \(HK=HI\)nên AC là đường trung trực của KI
hay AH là đường trung trực của HI hay tam giác AKI cân tại A
c) Vì tam giác AKI cân tại A nên \(\widehat{AKI}=\widehat{AIK}\)
Mà \(\widehat{BAK}=\widehat{AKI}\)(2 góc so le trong)
=> \(\widehat{AIK}=\widehat{BAK}\)
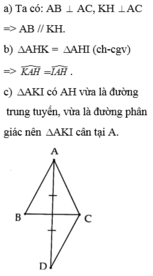
a: ta có: HK\(\perp\)AC
AB\(\perp\)AC
Do đó HK//AB
b: Xét ΔAHK vuông tại H và ΔAHI vuông tại H có
AH chung
HK=HI
Do đó; ΔAHK=ΔAHI
Suy ra: \(\widehat{KAH}=\widehat{IAH}\)
c: ta có: ΔAHK=ΔAHI
nên AK=AI
hay ΔAKI cân tại A
a)ta có: HK⊥AC
AB⊥AC
mà 2 góc này nằm ở vị trí so le trong
=> HK//AB
b: Xét ΔAHK vuông tại H và ΔAHI vuông tại H có
AH chung
HK=HI
=> ΔAHK=ΔAHI(g.h-c.g.v)
\(=>\widehat{HAK}=\widehat{HAI}\)
c)theo chứng minh câu B ta có
ΔAHK=ΔAHI
=> AK=AI (2 cạnh tg ứng)
=> ΔAKI cân tại A