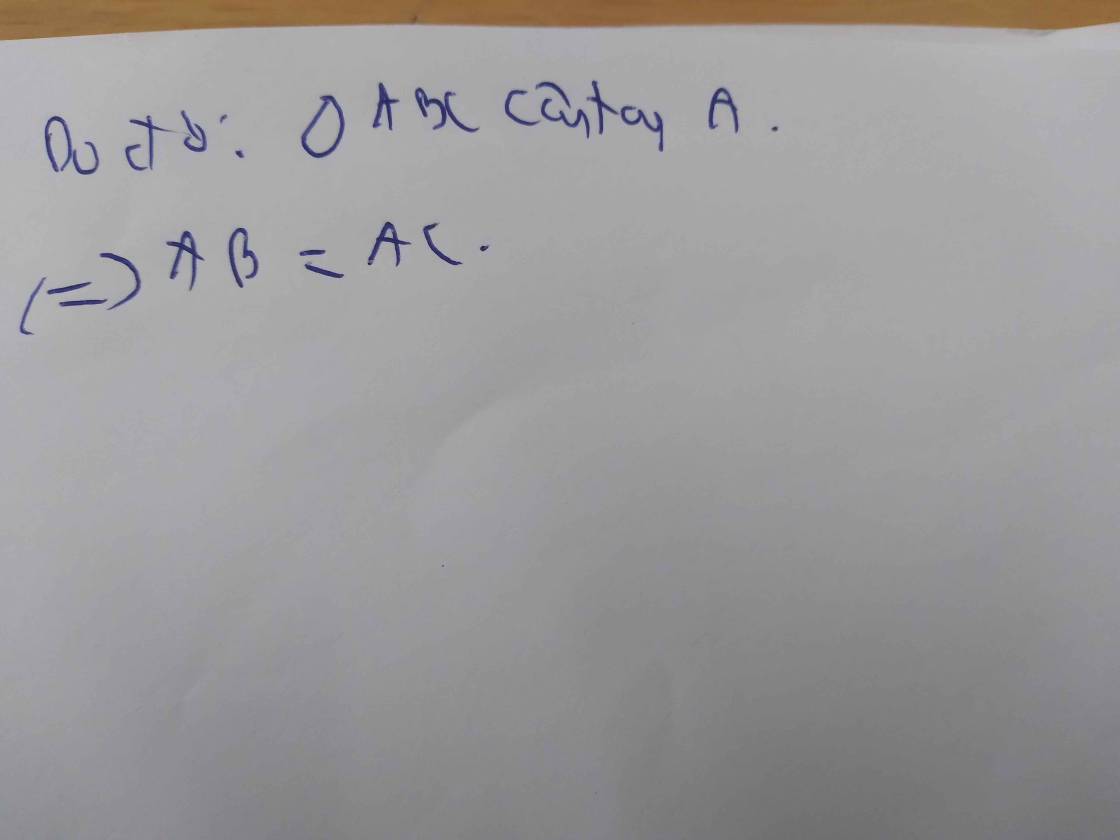Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét tứ giác AMCK có
I là trung điểm chung của AC và MK
góc AMC=90 độ
=>AMCK là hình chữ nhật
b: Xet tứ giác ABMK có
AK//MB
AK=MB
=>ABMK là hình bình hành
c; Xét tứ giác ABEC có
M là trung điểm chung của AE và BC
AB=AC
=>ABEC là hình thoi

b: Xét tứ giác ABDC có
M là trung điểm của AD
M là trung điểm của BC
Do đó: ABDC là hình bình hành
mà AD=BC
nên ABDC là hình chữ nhật

b: Xét tứ giác ABDC có
M là trung điểm của BC
M là trung điểm của AD
Do đó: ABDC là hình bình hành
mà AD=BC
nên ABDC là hình chữ nhật

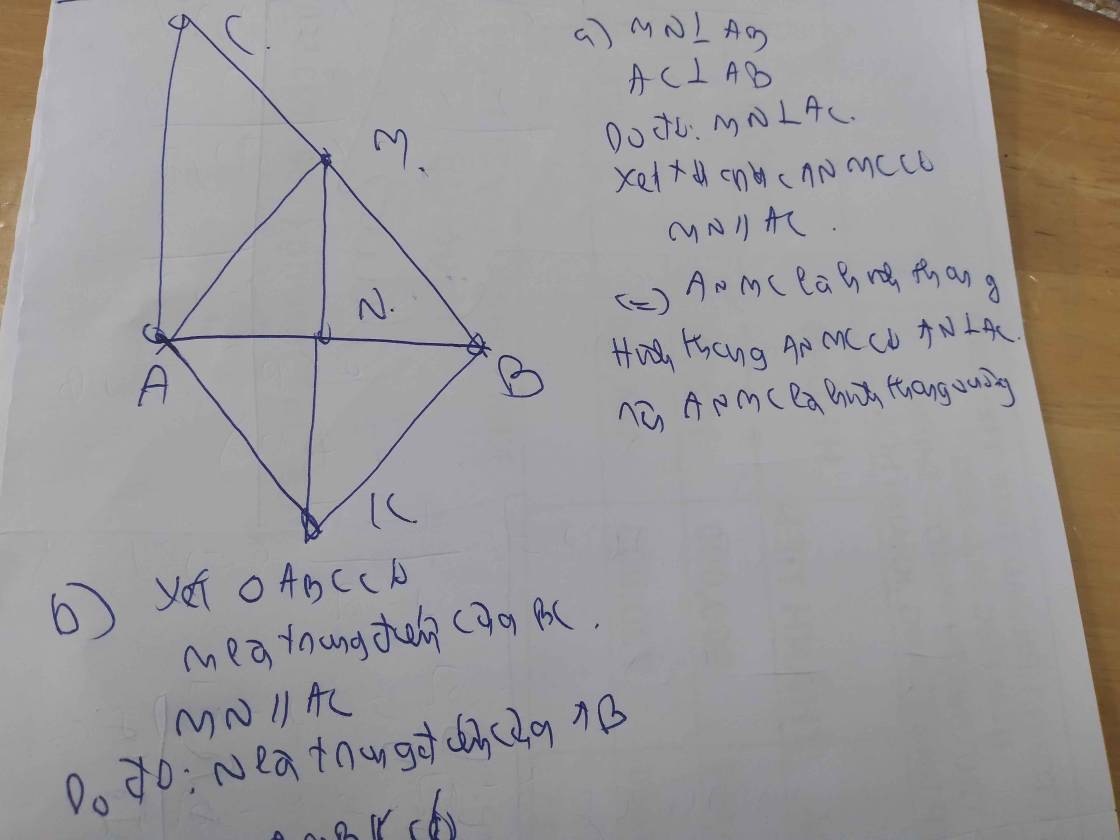
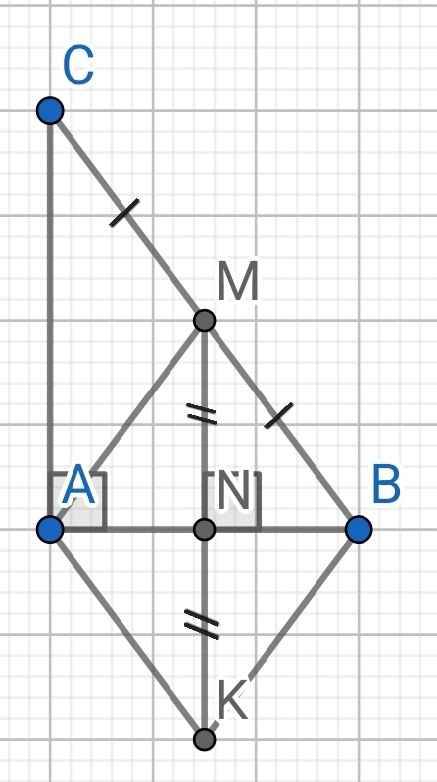 a) Do MN ⊥ AB (gt)
a) Do MN ⊥ AB (gt)
AC AB (do ∆ABC vuông tại A)
⇒ MN // AC
Tứ giác ANMC có:
MN // AC (cmt)
⇒ ANMC là hình thang
Mà ∠CAN = 90⁰
⇒ ANMC là hình thang vuông
b) ∆ABC có:
MN // AC (cmt)
M là trung điểm của BC
⇒ N là trung điểm của AB
Do MN ⊥ AB (gt)
⇒ MK ⊥ AB
Tứ giác AKBM có:
N là trung điểm của AB (cmt)
N là trung điểm của MK (gt)
⇒ AKBM là hình bình hành
Mà MK ⊥ AB (cmt)
⇒ AKBM là hình thoi
c) Để AKBM là hình vuông thì
AM ⊥ MB
⇒ AM ⊥ BC
⇒ AM là đường cao của ∆ABC
Mà AM là đường trung tuyến của ∆ABC (do M là trung điểm của BC)
⇒ ∆ABC có AM vừa là đường cao, vừa là đường trung tuyến
⇒ ∆ABC cân tại A
Mà ∆ABC vuông tại A (gt)
⇒ ∆ABC vuông cân tại A
Vậy để AKBM là hình vuông thì ∆ABC vuông cân tại A

a: Xét tứ giác ACDB có
M là trung điểm của BC
M là trung điểm của AD
Do đó: ACDB là hình bình hành
mà \(\widehat{BAC}=90^0\)
nên ACDB là hình chữ nhật

a: Xét tứ giác ACDB có
M là trung điểm của AD
M là trung điểm của BC
Do đó: ACDB là hình bình hành
mà \(\widehat{BAC}=90^0\)
nên ACDB là hình chữ nhật